简洁提示:通过生成过程中的连续简洁提示提升推理效率#
ConciseHint: Boosting Efficient Reasoning via Continuous Concise Hints during Generation
摘要#
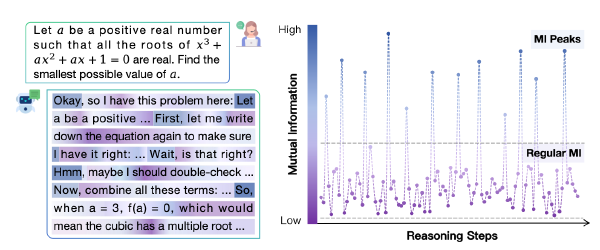
近期,诸如 DeepSeek-R1 和 OpenAI o1 系列等大型推理模型(LRMs)通过思维链(Chain-of-Thought, CoT)扩展生成长度,在复杂推理任务上实现了显著的性能提升。然而,一个新兴的问题是这些模型倾向于生成过度冗长的推理过程,从而导致效率低下的问题。现有的关于提升效率的研究主要遵循“推理前”范式,例如提示(prompting)加推理或微调(fine-tuning)加推理,却忽视了一个颇具前景的方向——在推理生成过程中直接鼓励模型进行简洁表达。为填补这一空白,我们提出了一种名为 ConciseHint 的框架,该框架在推理过程的 token 生成阶段持续注入文本提示(可人工设计或基于简洁数据训练得到),从而持续鼓励推理模型进行简洁表达。此外,ConciseHint 能够根据查询的复杂度自适应地调整提示强度,确保该方法不会损害模型性能。在包括 DeepSeek-R1 和 Qwen-3 系列在内的最先进 LRMs 上的实验表明,我们的方法能够有效生成更简洁的推理过程,同时保持良好的模型性能。例如,在 GSM8K 基准测试中,使用 Qwen-3 4B 模型,我们的方法在几乎无准确率损失的情况下,将推理过程长度减少了 65%。
Motivation#
- 过长 CoT 效率低
- LRM 通常生成不必要的连贯性 token,或执行冗余的自我验证
作者想要在生成中间推理步骤的过程中通过干预来引导 LRM 更简洁地表达
方法#
ConciseHint 在推理过程中(多次)注入类似 <|im_start|>make answer concise!<|im_end|> 的提示,例如原文是:
Okay, let me try to figure out this problem. The problem says a robe takes 2 bolts of blue fiber and half that much white fiber
则会被修改为
Okay,-<|im_start|>make answer concise!<|im_end|>- let me try to figure out this problem. The problem says a robe takes 2 bolts of blue fiber and half that much white fiber
注入强度#
过高的注入会损害 Acc,但是过少的注入就会导致效果没那么好。
所谓“注入强度”就是每次注入之间的 token 数量 \(\tau_k\)
定义如下:
$$ \tau_k = \alpha + \beta \cdot l_k, \alpha \gt 0, \beta \gt 0 $$其中 alpha 和 beta 为超参数,alpha 为基本注入间隔,实验中设置为 128,beta 设置为 0.2,l_k 是目前推理的长度。也就是说推理越长,注入间隔越大
为什么要这样设计呢?作者称基于“简单的问题可容忍的压缩率比复杂问题更大”这个假设,所以在 l_k 较小时,可以多多注入,但是当 l_k 长起来了,说明问题复杂了,需要减少注入频率
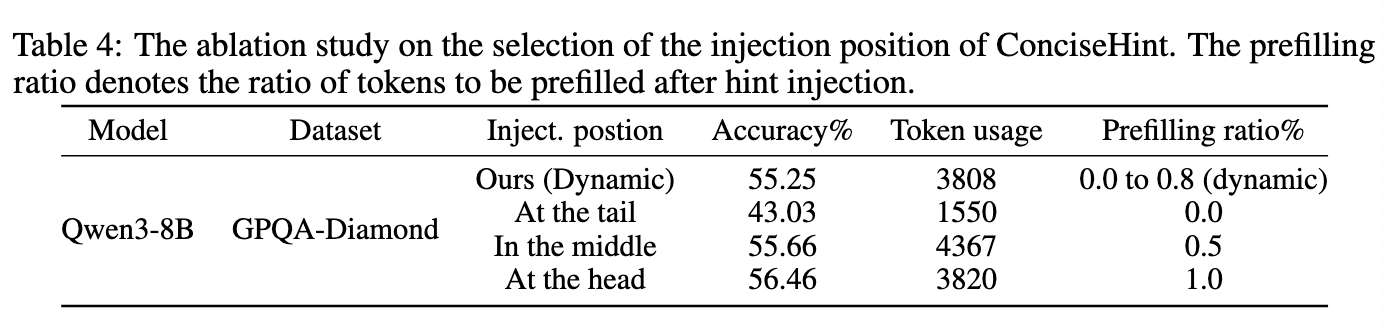
注入位置#
从实验中得出的规则:
- 在早期推理过程中,注入的位置不应当过于接近 Think 结束的位置
否则后续生成会很快结束推理,或者只是懒惰地重复上一个提示之后生成的文本。这显著降低了准确率
- 但是也不应该过于接近 Think 开始的位置
虽然将提示注入到开头能够解决准确率下降的问题,但它会引入额外的计算开销
于是设计插入位置如下:
$$ 插入位置=\tau_k \times min((\tau_k-\alpha)/1024, 0.8) $$修改提示词(AdaP)#
将一开始提示词换成“Please adaptively control the answer length based on the query’s complexity. The lower the complexity, the more concise your answer should be”
但是如果将 AdaP 应用在注入的提示词上,可以获得更好的效果
训练 Embedding#
先准备一个包含问题及其相应简洁推理回答的数据集,然后通过在原始回答中以固定间隔注入待训练的 hint embedding,构建修改好的推理回答。进行 SFT。E_{ori}是在 ConciseHint 中手动设计的 Hint Embedding,训练后得到优化后的提示嵌入 E_{optim}
$$ E_{interp}=\alpha \times E_{optim}+(1-\alpha) \times E_{ori}, 0 \le \alpha \le 1 $$这种方法记为 ConciseHint-T
实验#
Training free#
数据集:GSM8K、AIME24、GPQA-Diamond
模型:Qwen3-8B、Qwen3-4B、Qwen3-1.7B、DeepSeek-R1-14B
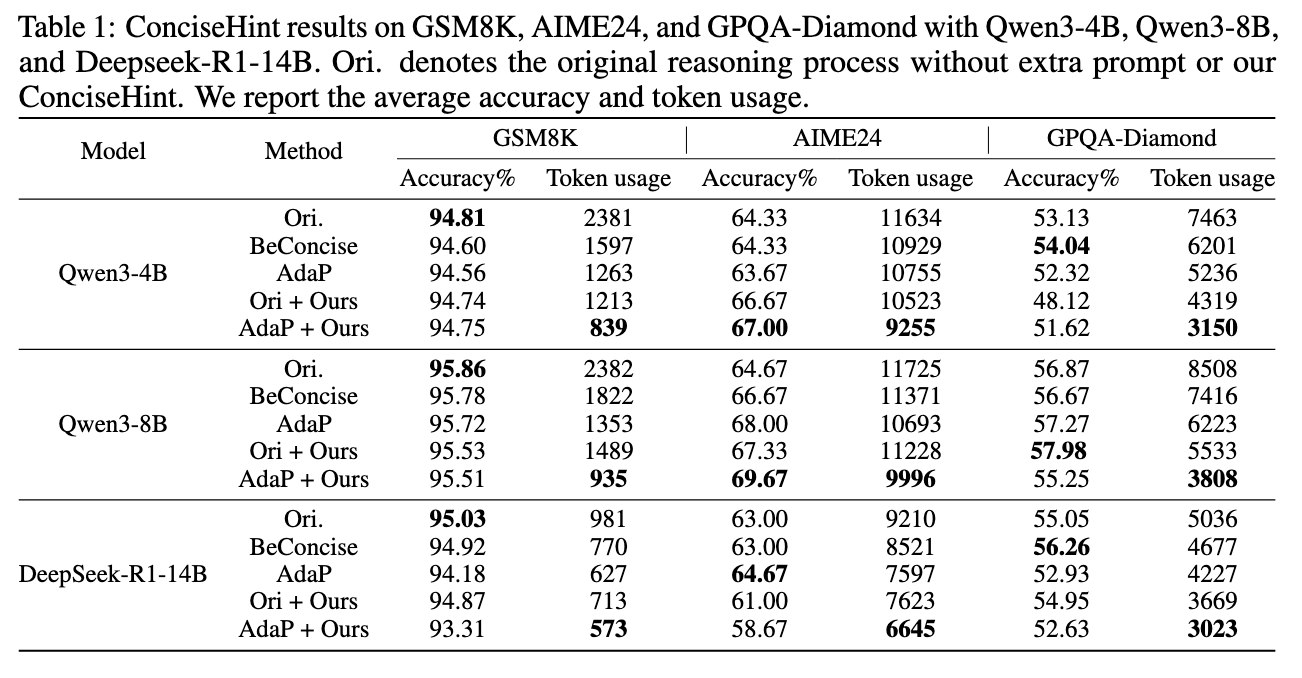
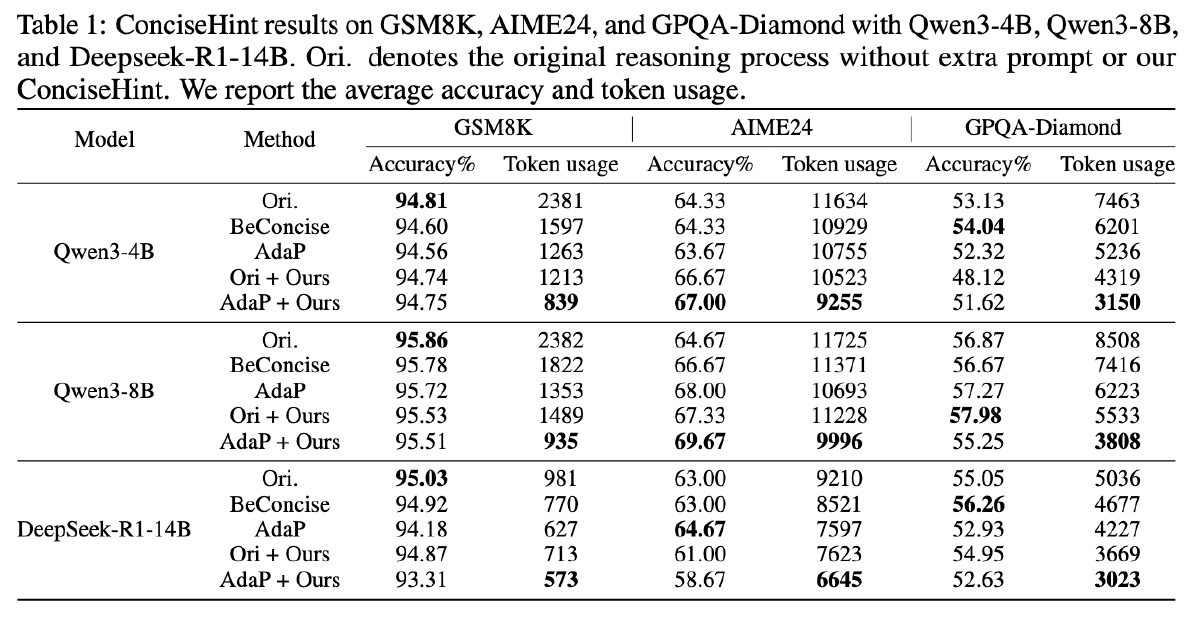
Ori 为原始模型
BeConcise 是在一开始输入的提示词中添加“Be concise”
AdaP 是在一开始输入的提示词中添加“Please adaptively control the answer length based on the query’s complexity. The lower the complexity, the more concise your answer should be”
Ori+Ours 是将**-<|im_start|>make answer concise!<|im_end|>-** 插入思考过程
AdaP+Ours 是将**-<|im_start|>Please adaptively control the answer length based on the query’s complexity. The lower the complexity, the more concise your answer should be<|im_end|>-** 插入思考过程
Training#
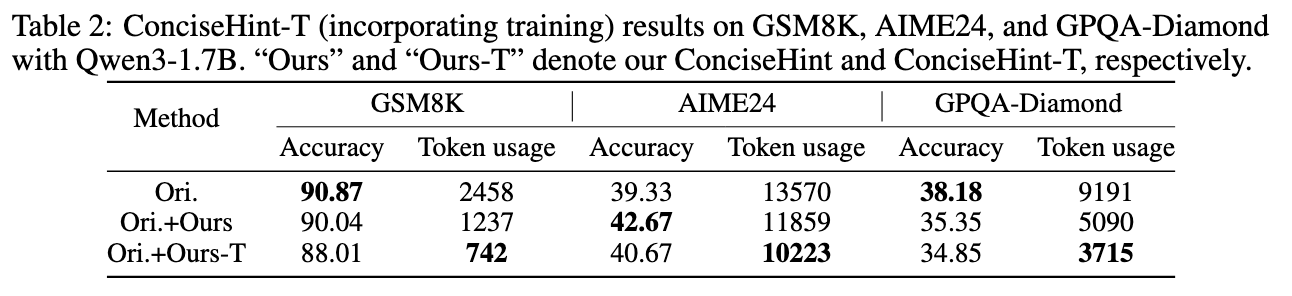
其他#
不同超参数:
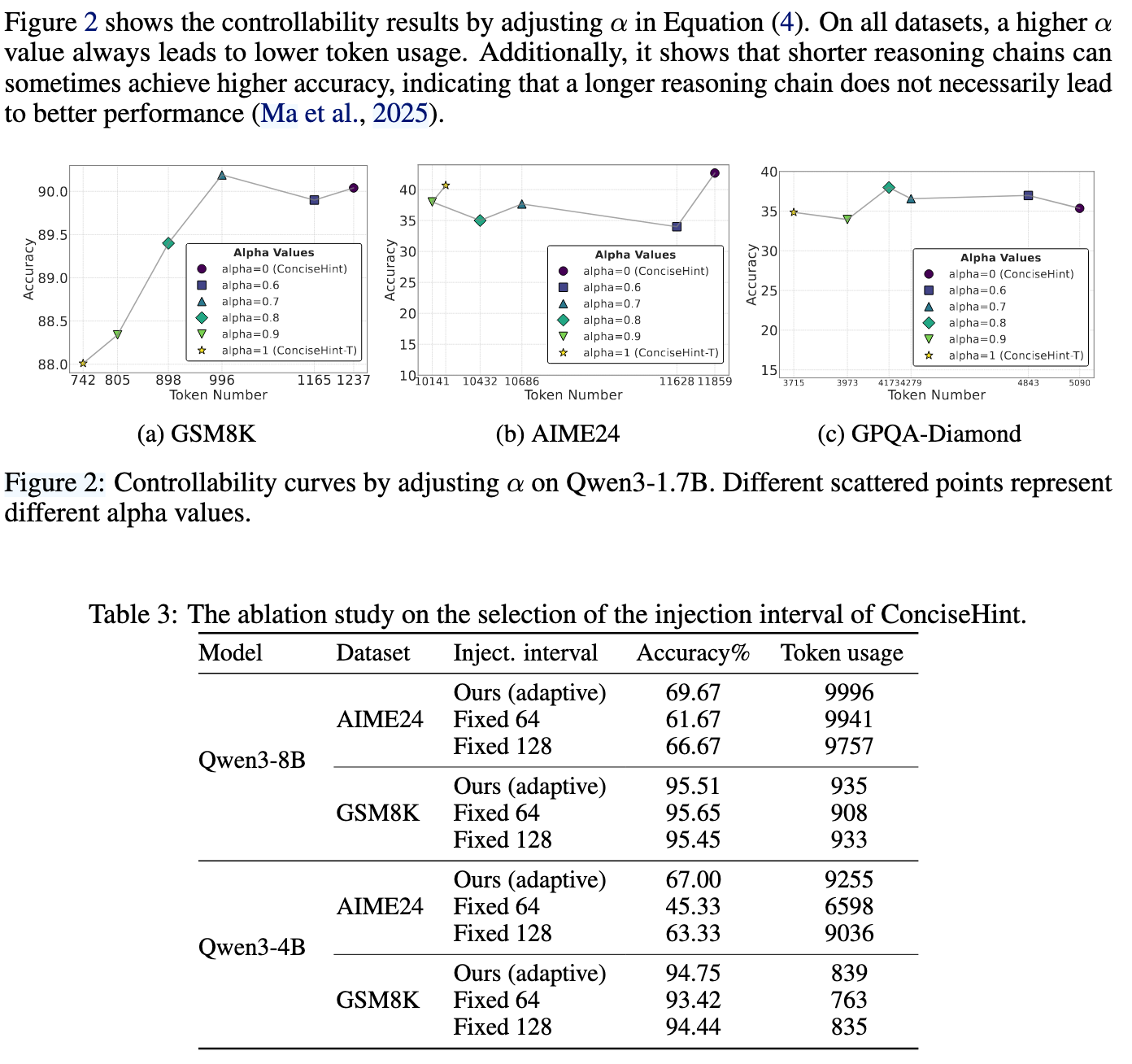
在不同地方插入提示