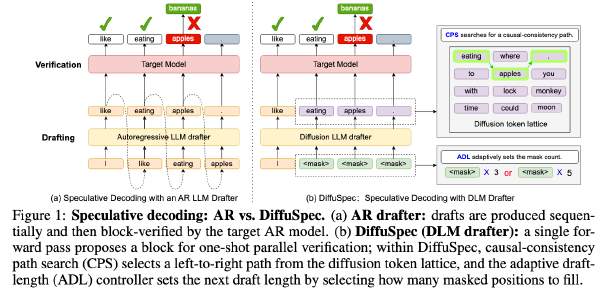
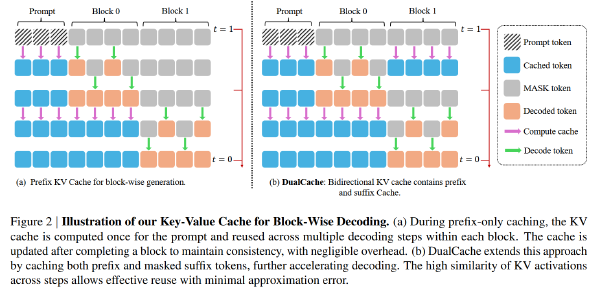
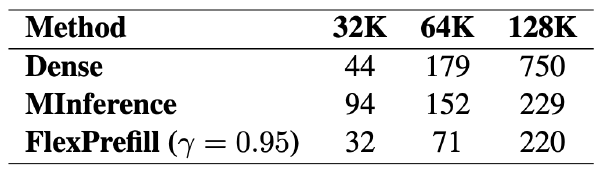
面向大语言模型的门控注意力机制：非线性、稀疏性和Attention-Sink-Free

面向大语言模型的门控注意力机制：非线性、稀疏性和 Attention-Sink-Free
#

摘要
#

门控机制已被广泛应用于从早期模型如 LSTM 和 Highway Networks，到近期的状态空间模型、线性注意力，以及 softmax 注意力。然而，现有文献很少深入探讨门控的具体作用。在本研究中，我们通过全面实验系统性地探究了引入门控的 softmax 注意力变体。具体而言，我们在一个包含 3.5 万亿 token 的数据集上训练了 30 种 15B 规模的 Mixture-of-Experts（MoE）模型和 1.7B 规模的密集模型，并进行了详尽比较。我们的核心发现是：一种简单的修改——在 SDPA 之后应用每个注意力头独立的 sigmoid 门控——能够持续提升模型性能。该修改还增强了训练稳定性，允许使用更大的学习率，并改善了模型的扩展特性。通过对多种门控位置和计算变体的比较，我们将此效果归因于两个关键因素：（1）在 softmax 注意力中的低秩映射上引入非线性；（2）使用依赖于查询的稀疏门控分数来调节 SDPA 的输出。值得注意的是，我们发现这种稀疏门控机制能够缓解“attention sink”现象，并提升长上下文外推能力。我们同时公开了相关代码和模型，以促进后续研究。

Motivation
#

尽管门控机制已被广泛采用并取得经验上的成功，但其功能与影响仍超出初始直觉之外，尚未得到充分探索。而这种理解不足，影响了对其利用

理解不足阻碍了对门控机制真实贡献的评估，尤其是在其与其他架构因素混杂的情况下。例如，尽管 Switch Heads（Csordas 等，2024a;b）引入了 sigmoid 门控以选择前 K 个注意力头专家，但我们的实验揭示了一个有趣的发现（附录 A.1）：即使缩减为单个专家，其中门控仅简单地调节 value 输出，仍然存在显著的性能提升。这强烈表明门控机制本身具有重要的内在价值，独立于路由机制之外。类似地，在 Native Sparse Attention（NSA）（Yuan 等，2025）中，尽管展示了整体性能的提升，但并未将门控机制的贡献与稀疏注意力设计本身的效果区分开来。这些考量突显了严格分离门控效应与其他架构组件影响的必要性。

前置知识
#

注意力
#

注意力是基于 QKV 三个矩阵计算出来的，可以理解为最终结果是对于 V 乘上了一个权重（相当于对于出 V 矩阵中重要的值乘以更高的权重，不那么重要的则乘以较低的权重）

$$ Attn(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V $$

其中 d_k 注意力头的维度，除以这个是为了对于注意力进行缩放，用于稳定方差和梯度

自注意力
#

自注意力顾名思义，就是自己对于自己的注意力。具体而言，就是 Q、K、V 都来自同一个输入 X

$$ Q=W_QX,K=W_KX,V=W_VX $$

然后带入上面计算 Attn 的式子中计算自注意力

$$ SelfAttn(X)=softmax(\frac{W_QX(W_KX)^T}{\sqrt{d_k}})W_vX $$

多头自注意力和最终输出
#

指在一个层中，使用不同的 W_Q/W_K/W_V 计算出不同的 SelfAttn 的结果，用于提取/处理不同的信息。其中每一组 W_Q/W_K/W_V 构成一个头。将一层内多个头的计算结果拼接起来之后，一起乘上一个 W_O，就差不多可以作为这一层的输出了。

实际还有残差连接、FFN 和 Norm 等操作

例如 Qwen3-8B，共 36 层、每层有 32 个头，伪代码表示如下

下面的伪代码仅用于大概展示 Transformer 的工作原理，实际不同模型的 Norm、FFN、残差连接等操作的顺序和次数可能不太一致，例如 Qwen 的架构就采用的前置 Norm，而非下面伪代码展示的后置 Norm

## 输入 X: 形状通常为 [Batch_Size, Seq_Length, Hidden_Dimension]
for each_layer in layers: # Qwen3-8B 共 36 层
    # 多头自注意力机制
    head_outputs = []
    # 实际代码实现中，每个头的计算是并行的，也不需要下一步的拼接
    for each_head in each_layer.heads:  
        attn_of_this_head = each_head(X)
        head_outputs.append(attn_of_this_head) 
    concat_output = concatenate(head_outputs) 
    attention_output = each_layer.W_O_linear(concat_output) 
    
    # 文字中省略的其他部分
    # 残差连接
    X_after_attn = LayerNorm(X + attention_output) 
    # 前馈神经网络 (FFN） 
    ffn_output = each_layer.ffn(X_after_attn)
    # 再次残差连接 + 归一化
    X = LayerNorm(X_after_attn + ffn_output)
return X

使用门控机制增强的 Attn
#

设计一个门函数

$$ Y'=Y \boxed{?} Activate(XW_\theta) $$

其中 X 不同于用户输入的 X，这里的 X 指用于调整门控指的输入（在实验中，作者使用 Norm 之后的隐藏状态作为 X），$W_\theta $ 是一个 linear 层

作者 huggingface 上说采用的是 Qwen3 架构，Qwen3 是前置 Norm，所以可以将 Norm 之后的东西作为 X 输入门

其中 $\boxed{?}$指一种运算方式，因为作者实验中设计了不同的计算方式，这里将其模糊处理

其中$Activate$是一种激活函数，同样因为作者实验中采用了不同的激活函数，这里模糊处理

实验
#

Settings
#

作者进行了以下几组实验：

不同位置施加门（G1~G5)

施加门的粒度：$XW_\theta $ 是标量 or 和 Y 同尺寸的矩阵
每个头共享一个$W_\theta $ or 每个头有自己的$W_\theta $
乘法（$Y'=Y \odot Activate(XW_\theta)$） or 加法（$Y'=Y + Activate(XW_\theta)$）门控
激活函数：$Activate=SiLU$ or $Activate=Sigmod$

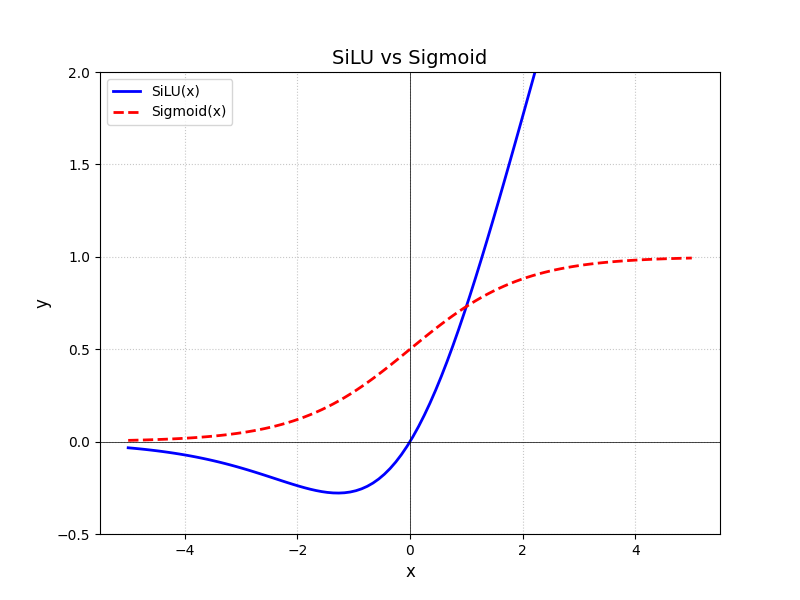
由于 SiLU 无上界，所以在实验中 SiLU 仅用在了加法门控中

代码里能看到，是对于每一层都应用了各自的 Gate

模型、设备、超参、数据等
#

模型：15A2.54B（128 个总专家、top-8 softmax 门控机制、细粒度专家、全局批处理 LBL、z-loss）、1.7B 两个模型

细粒度专家：专家参数量较少，比如这个模型，总共 15B 的参数拆出了 128 个专家全局批处理：在计算 Loss 时，不再局限于单卡，而是统计全局一个 Batch 中的 Token 分布。可以让全局大 batch 中同时均衡覆盖各种不同任务，能提高 MoE 训练的效果 z-loss：在 MoE 训练的时候，router 参数的改变会导致 loss 飙升，于是谷歌设计了 z-loss 来解决这个问题

数据集：

训练：应该是一个内部数据集（我们在一个包含 3.5T 高质量 token 的子集上训练模型，涵盖多语言、数学和通用知识内容）
测试（few-shots）：Hellaswag（英语）、MMLU（通用知识）、GSM8k（数学）、HumanEval（代码）、C-eval 和 CMMLU（中文），以及多种内部数据集

超参：Context Length=4096

模型	学习率	Batch size	step
MoE-15A2.54B	1k步内预热到2e-3 余弦退火到3e-5	1024	100k
1.7B（400B Token）	最大学习率 4e-3	1024
1.7B（3.5T Token）	最大学习率 4.5e-3	2048

算法备注：Attention 部分采用组查询注意力

组查询注意力指多个 Query 头共享一组 KV 头，和 baseline 性能接近，但是降低显存和提高速度比如在 n 个注意力计算的公式中，n 个 W_K 是固定的一个 linear、n 个 W_V 固定一个 linear，但是 n 个 W_Q 是 n 个 linear

结果
#

MoE-15A2.54B
#

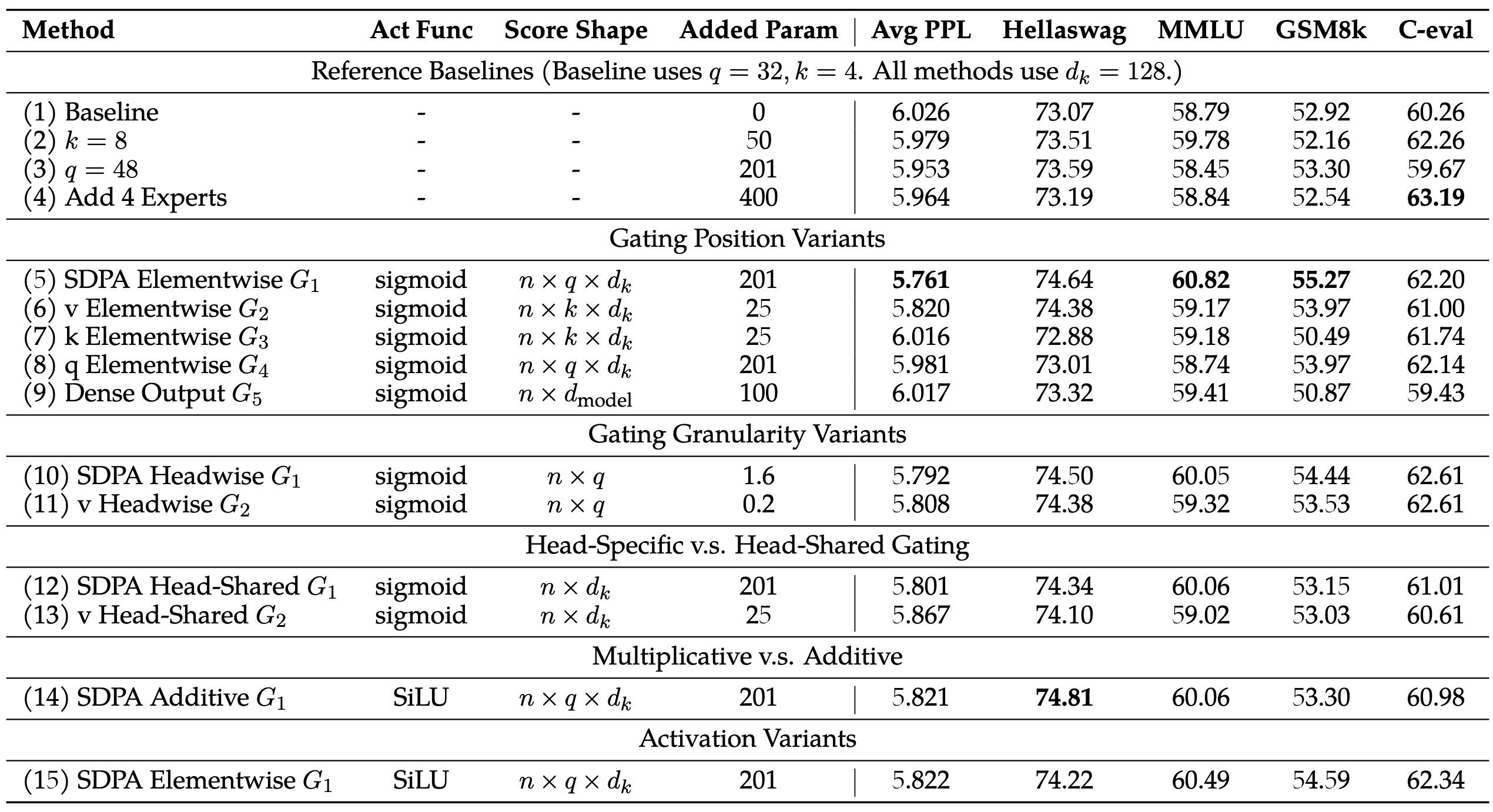
在 G1 和 G2 处添加门控是最有效的
不同粒度差别不大、分头还是 Head Shared 差别不大
乘法比较好
Sigmod 比 SiLU 好

1.7B
#

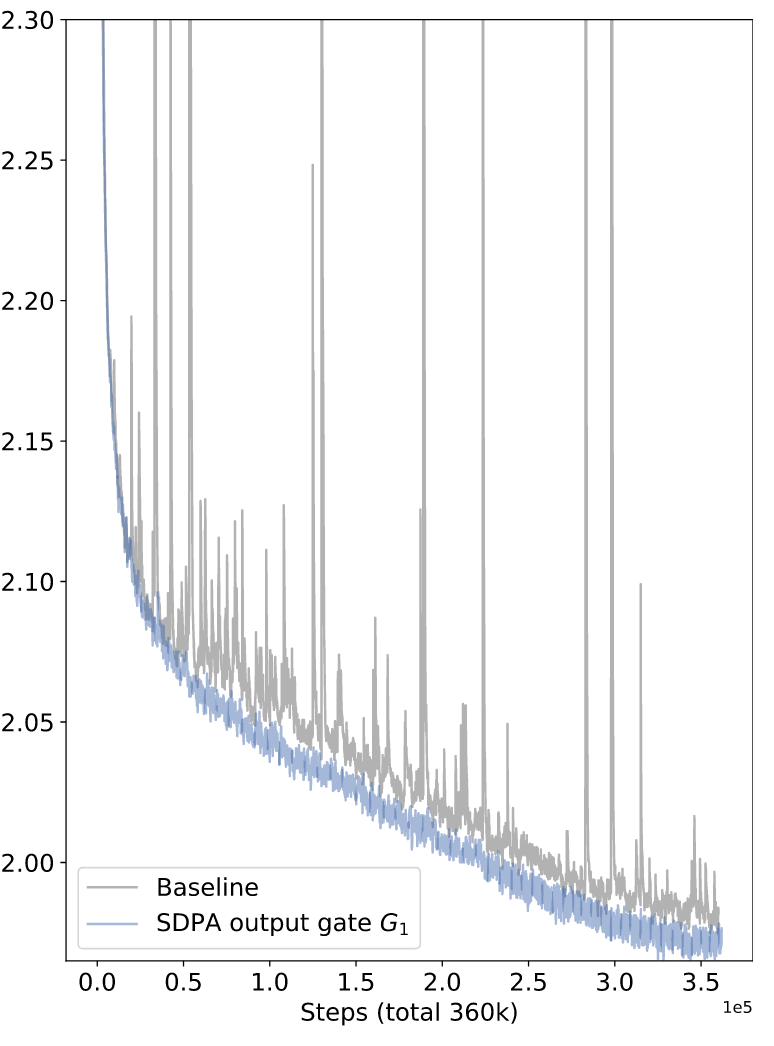
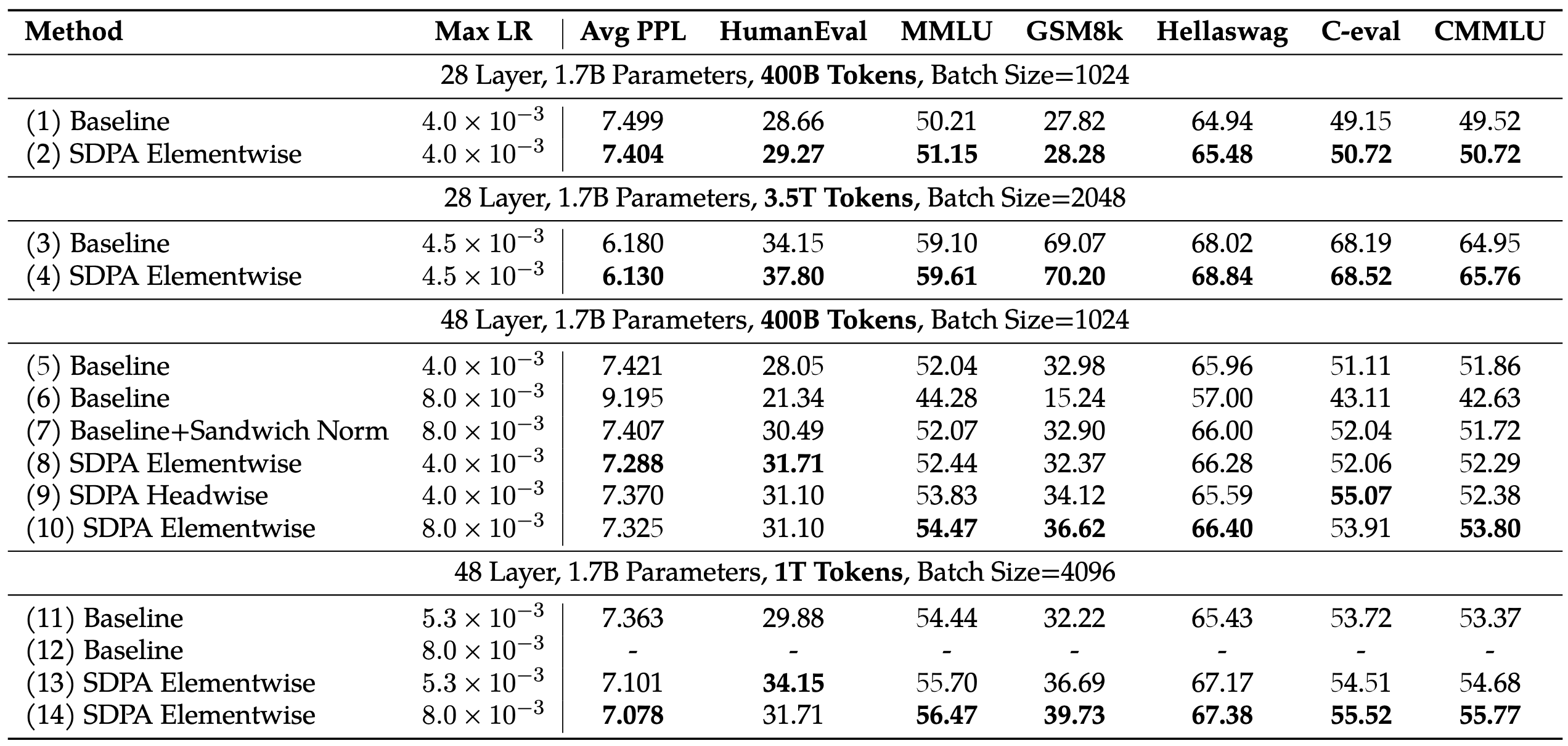
作者另外发现使用门控机制可以大大提高训练的稳定性，减少 Loss 峰值的出现，于是可以继续使用更大的模型参数、大学习率、大 Batch Size 获得性能又好、训起来又快的模型

分析
#

作者将门控机制提升性能，归结为两个主要原因：

门控的非线性运算提升了模型性能
门控引入了强输入依赖的稀疏性，降低了 Attention Sink 问题

非线性运算提升模型性能
#

在多头注意力中，第 i 个 token 和第 k 个头的对应关系如下：

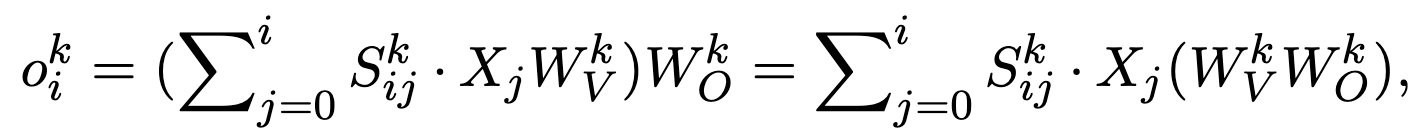
可以看到，W_V 和 W_O 是直接相乘的，缺乏非线性变换，而 G1 和 G2 相当于在 WV 和 WO 之间应用了非线性变换，所以性能提升了，而其他门控变化不大

同时作者进行了消融实验，发现仅在 SDPA 输出后加 RMSNorm（无额外参数）也能显著降低 PPL

强输入依赖的稀疏性
#

作者分析了门控分数的分布，发现 SDPA 输出门控分数大多分布集中在 0 附近、少数 long tail 到 1，是稀疏的
G1 门控分数取决于当前的 Query，模型可以根据 Query 再进一步过滤信息，而 G2 这种直接对 Value 做 Gate 的效果并不好

我个人觉得这个解释比较牵强，G1 的 Input 是 X 的隐藏状态和 MultiHead 的结果，为什么说它和 Query 是强关联的？我觉得可以解释成，G1 相当于基于 X 又进行了一次 Query

作者做了消融实验，将 Sigmod 函数换成一个非稀疏版本的 Sigmod，发现相比直接用 Sigmod 性能下降

$$ NSSigmod(x)=0.5+0.5Sigmod(x) $$

门控缓解了 Attention Sink 现象
#

什么是 Attention Sink 现象
#

有研究者发现，LLM 深层的时候，倾向于给第一个 Token 分配更高的注意力（如下图）

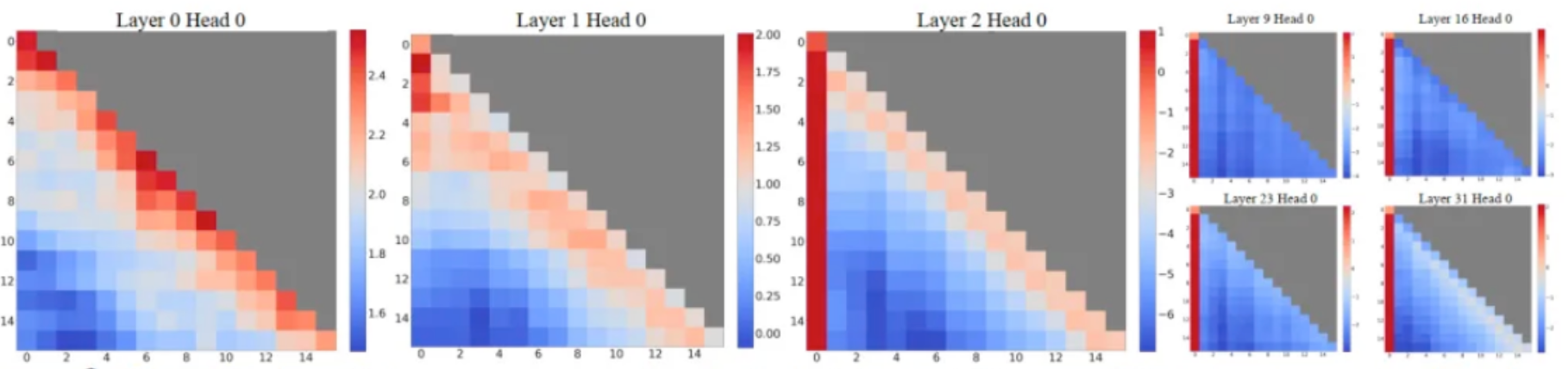
有一个解释如下：

LLM 在浅层时已经完成了信息的处理，所以后续如果再融合输入的 token 的信息反而会降低输出的质量，于是模型就需要获取尽可能少的信息。而由于传统模型是因果的，后面的 Token 能够看到前面的 Token，因此后面的 Token 中是包含前面的 Token 的信息的。因此，在深层，LLM 倾向于将 Attention 放到信息最少的 Token 上面，也就是第一个 Token/最开始的几个 token

作者发现，使用稀疏的门控 G1 可以大大降低 Attention Sink 现象，而不那么稀疏的 G2 或者使用了 NS-Sigmod 激活函数的 Gate 的 Attention Sink 的现象会很明显

使用门控有利于模型 Context 扩展
#

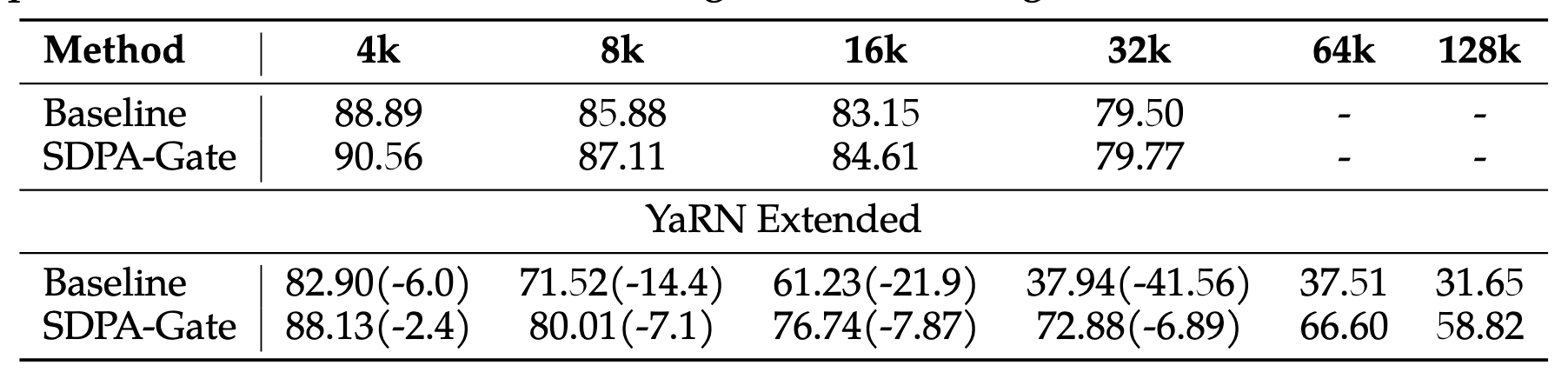
作者分析 Baseline 依靠 Attention Sink 来消耗多余的注意力，但是当应用 YaRN 时，这种方式就被破坏了，导致 Baseline 性能大幅下降，而使用 G1 可以在模型的 Attention 输出中挑拣出需要的信息，模型就不需要依赖 Attention Sink 了，因此性能下降小于 Baseline

YaRN 的做法是什么
#

随着序列长度增加，QK^T 会大大增加

长度增加则让 Q 和 K 的整体方向更接近，导致 QK^T 结果更大，因此需要对于 Attention 进行缩放

YaRN 是修改 Attention 计算方式为：$Attn=Softmax(\frac{QK^T}{t\sqrt{d}})V$，其中 t 被称为温度系数，YaRN 作者提出了一个经验值$t=\frac{ln(s)}{10}+1$，S 指缩放因子，比如 32K 上下文缩放到 128K，S=128/32=4

所以 YaRN 和 Attention Sink 就具有天生的冲突，Attention Sink 将大量 Attention 消耗到 First a few token 上，但是 YaRN 又将这个尖锐的 Attention 拉回来了

Saber：一种针对扩散语言模型的自适应加速与回溯增强的高效采样方法

2025 Nov 7·1125 字·3 分钟

算法论文论文算法

Saber：一种针对扩散语言模型的自适应加速与回溯增强的高效采样方法 # Saber: An Efficient Sampling with Adaptive Acceleration and Backtracking Enhanced Remasking for Diffusion Language Model