面向模型推理思考优化的 Test time scaling#
Towards Thinking-Optimal Scaling of Test-Time Compute for LLM Reasoning
摘要#
近期研究表明,让模型花费更多时间通过更长的 Chain of Thoughts(CoTs)可以显著提升其在复杂推理任务中的表现。尽管目前的研究仍在继续探索通过扩展 Large Language Models(LLMs)的 CoT 长度来增加测试时计算量的好处,但我们关注到当前追求测试时扩展可能隐藏的一个潜在问题:过度扩展 CoT 长度是否真的会对模型的推理性能带来负面影响?我们在数学推理任务上的探索揭示了一个意外发现,即在某些领域中,过度使用更长的 CoTs 确实会损害 LLMs 的推理能力。此外,我们还发现存在一个在不同领域中有所差异的最佳扩展长度分布。基于这些洞察,我们提出了 ThinkingOptimal Scaling 策略。我们的方法首先使用一组具有不同响应长度分布的小规模种子数据,教导模型根据不同推理需求采取不同的思考努力;然后,模型在额外的问题上,根据不同的推理努力选择最短的正确回答进行自我改进。我们的自优化模型基于 Qwen2.5-32B-Instruct 构建,在各种数学基准测试中超越了其他基于蒸馏的 32B o1 类模型,并且性能达到了与 QwQ-32B-Preview 相当的水平。
Motivation#
类似 o1 的模型会出现 over-thinking 迹象、且更长的 CoT 可能对模型性能产生负面影响(研究问题)
我们的目标是探讨和研究过度的测试时扩展是否可能损害大型语言模型(LLMs)在数学领域中的推理性能。
研究问题 1——过长 CoT 影响 llm 性能#
实验 1#
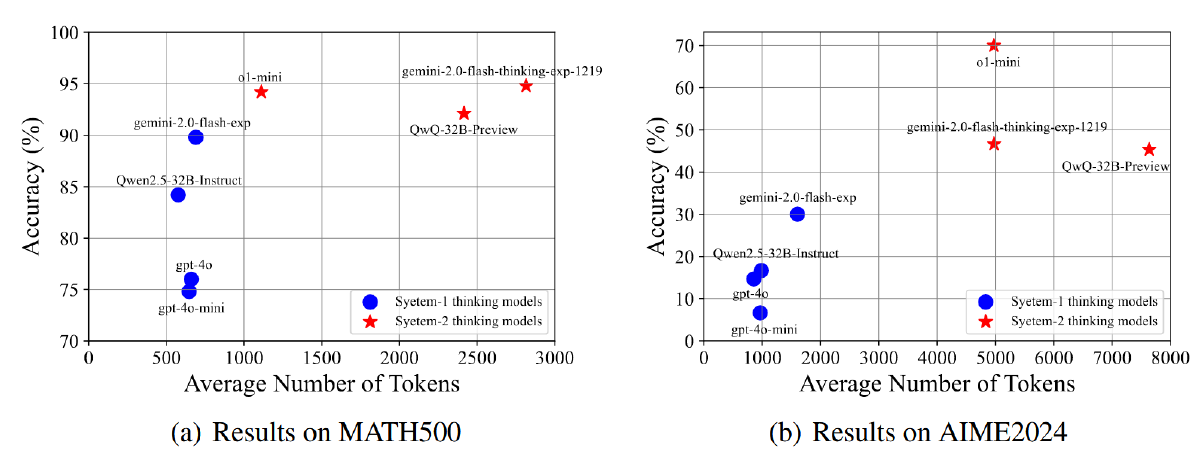
使用 MATH500 和 AIME2024 数据集,统计平均 token 数,使用 Qwen2.5 tokenizer 计算每个模型生成的 CoTs 的 token 数量以进行公平比较。
对于无法获取内部 CoT 的模型(如 o1-mini),使用 summary、推理 token 数和总补全 token 数估计 token 数,
\(n^{qwen}_s\)代表 qwen tokenizer 估计出的 token 数, \(n^{o1}_r\)代表 o1 返回的 Reasoning token 数, \(n^{o1}_c\)代表 o1 返回的 summary token 数 + \(n^{o1}_r\)
$$ token总数=n^{qwen}_s \times \frac{n^{o1}_r}{n^{o1}_c - n^{o1}_r} $$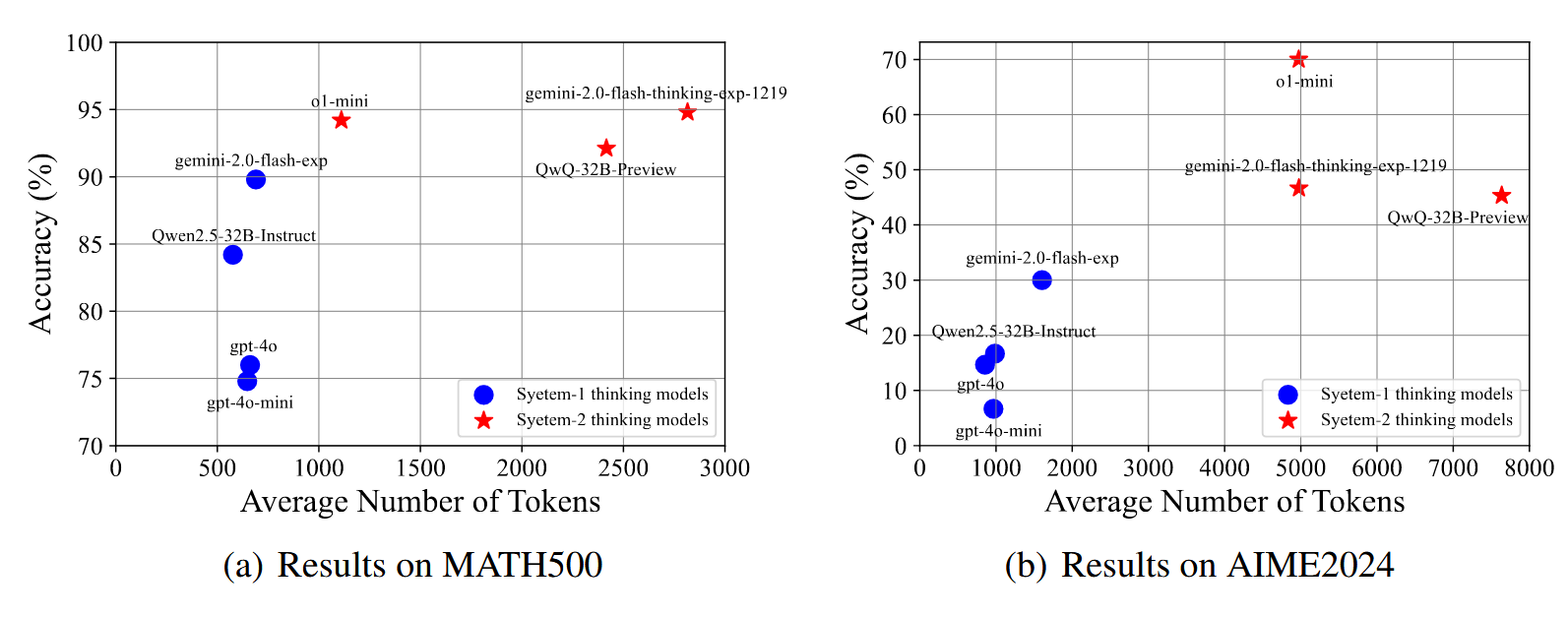
后续的 o1-like 模型(QwQ32B-Preview 和 Gemini2.0-Flash-Thinking)相比于 o1-mini 显示出较少的有效扩展效果,因为它们生成了更多的 token,但在从其对应的 System-1 思维模型扩展时获得的改进却更少。QwQ-32B-Preview 在这方面存在最严重的问题。这一初步分析在一定程度上表明,过度扩展到更长的 CoT 并不能最大化测试时间的扩展效果。
实验 2#
- 使用三个 system prompt,对应不同努力程度(“低”、“中”、“高”),让 QwQ-32B-Preview 为从 NuminaMath 数据集中的问题生成不同数量 token 的解决方案

- 筛选出在三种推理努力下均正确回答且推理路径长度不同的问题,
QwQ-32B 的指令跟随能力相对较差,体现在对同一问题生成的响应长度分布与指定的系统提示不完全匹配。对于给定的问题,进一步根据三个响应的长度重新排序,并在它们的成对长度差异始终超过 300 个 token 时保留它们。
- 使用上述所有 问题-推理-答案 数据微调 LLaMA3.1-8B 和 Qwen2.5-32B,命名为 LLaMA3.1-8B-Tag 和 Qwen2.5-32B-Tag。
Finally, we curate a set of 1.3K problems, each accompanied by three o1-like responses of varying lengths. The data statistics of each set for each model is shown in Table 1.
没懂,是使用不同的数据集微调模型吗?

lr=1e-5,batch_size=32, Qwen 的 epochs 为 3, LLaMA 为 5
- 对于 Tag 模型,分别使用三种提示词,测试问题回答
o1-like model temperature 设置为 1.0。对于 Qwen 和 LLaMA 分别比较 temperature 为 1.0 和 0.0 的情况,对于 temperature 为 1.0 计算 5 次随机 seed 的平均值
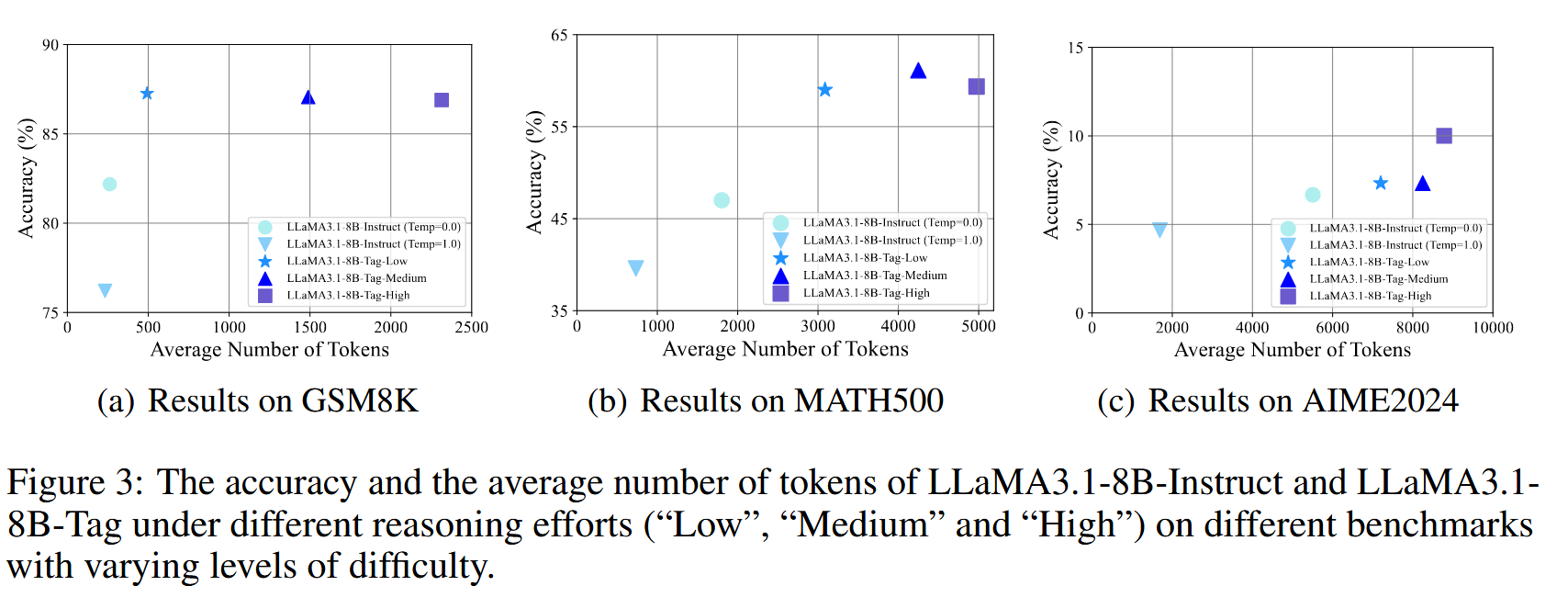
在 GSM8K 和 MATH500 数据集上,不同的 Token 数得出的 Acc 相差不大,但是在 AIME2024 上相差较多
我们可以从这些结果中得出几个有趣的结论:
- 少量的 o1-like 响应已经能够显著提升 LLMs 的推理性能,这与之前的研究结果一致[22, 14]。
- 在某些领域,特别是简单任务上,随着 CoT 长度的增加可能会对模型的推理性能带来负面影响。例如,LLaMA3.1-8B-Tag 和 Qwen2.5-32B-Tag 在高推理努力下表现不如其他两种推理努力,同时消耗了显著更多的 token,特别是在 GSM8K 和 MATH500 数据集上。
- 存在一个最佳的推理努力程度,它因任务难度的不同而有所差异。正如我们所见,在 GSM8K 上低推理努力始终表现最佳,而在较难的问题上,中等和高推理努力则更为有益。
分析——为什么过长 CoT 反而会影响性能?#
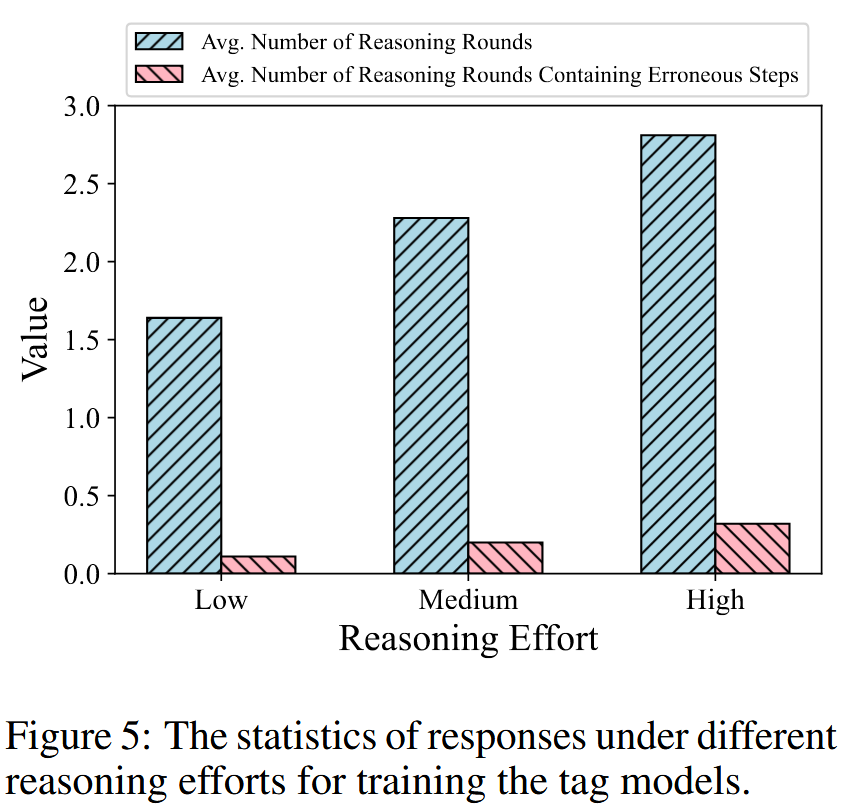
我们观察到当推理努力增加时,错误推理轮次的数量也增加。在更多错误步骤上训练模型会对模型的推理能力带来负面影响,这可以解释为什么高推理努力的扩展会导致更差的结果。因此,我们可以得出结论,虽然包含某些错误且具有反思性的步骤可以帮助模型在推理过程中学习纠正错误,但过多的错误步骤可能会对模型的学习产生有害影响。
研究问题 2——Thinking-Optimal Test-Time Scaling#
简称 TOPS
主要解决,如何让 llm 在复杂问题上投注更多精力(更长的 CoT),在简单问题上少一点
方法#
格式模仿-有条件的不同努力推理生成-自我改进
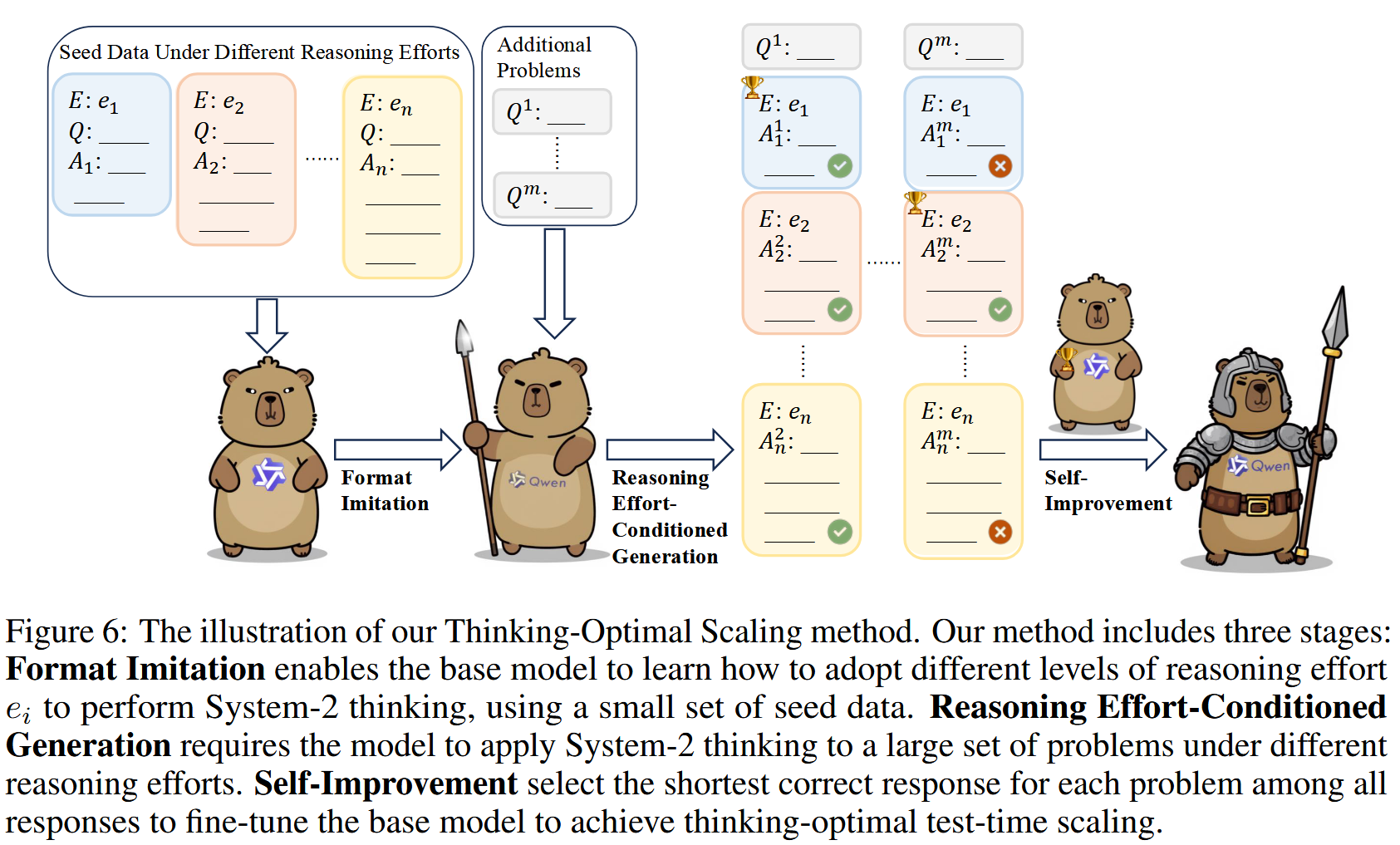
格式模仿#
一组 o1-like 的回复进行冷启动,使模型可以学习 system 2 的思维模式,可以由人工书写 or 模型生成,后续实验中选择 QwQ-32B-Preview 的不同努力程度的思维链
但是以往研究采用的是固定长度分布的 seed sample(即直接由现有的 o1 类模型生成),本篇工作选择创建包含不同推理努力下的响应的种子数据(即不同的长度分布)。
作者构建数据集
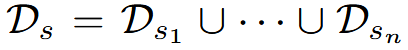
其中 D_{si}表示在特定推理努力 ei 下对种子问题的响应。
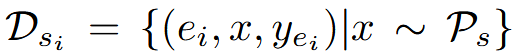
并基于此数据集训练基础 tag 模型
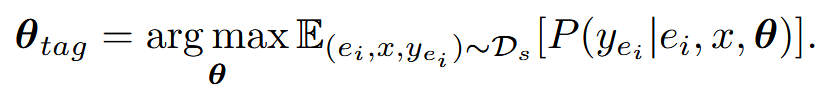
有条件的不同努力推理生成#
然后我们使用标记模型在不同的推理努力 ei 下为大量的额外数学问题 Pa 生成解决方案。
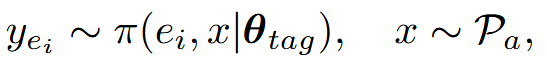
其中 π 是 tag 模型(使用上述数据集微调出的模型)的输出分布。接着在所有的 Pa 的 y 中选择正确的且最短的 y,作为 Pa 的 thinking-optimal response,基于此构建了一个数据集
自我改进#
基于上述构建的数据集,再 SFT 基础模型
实验#
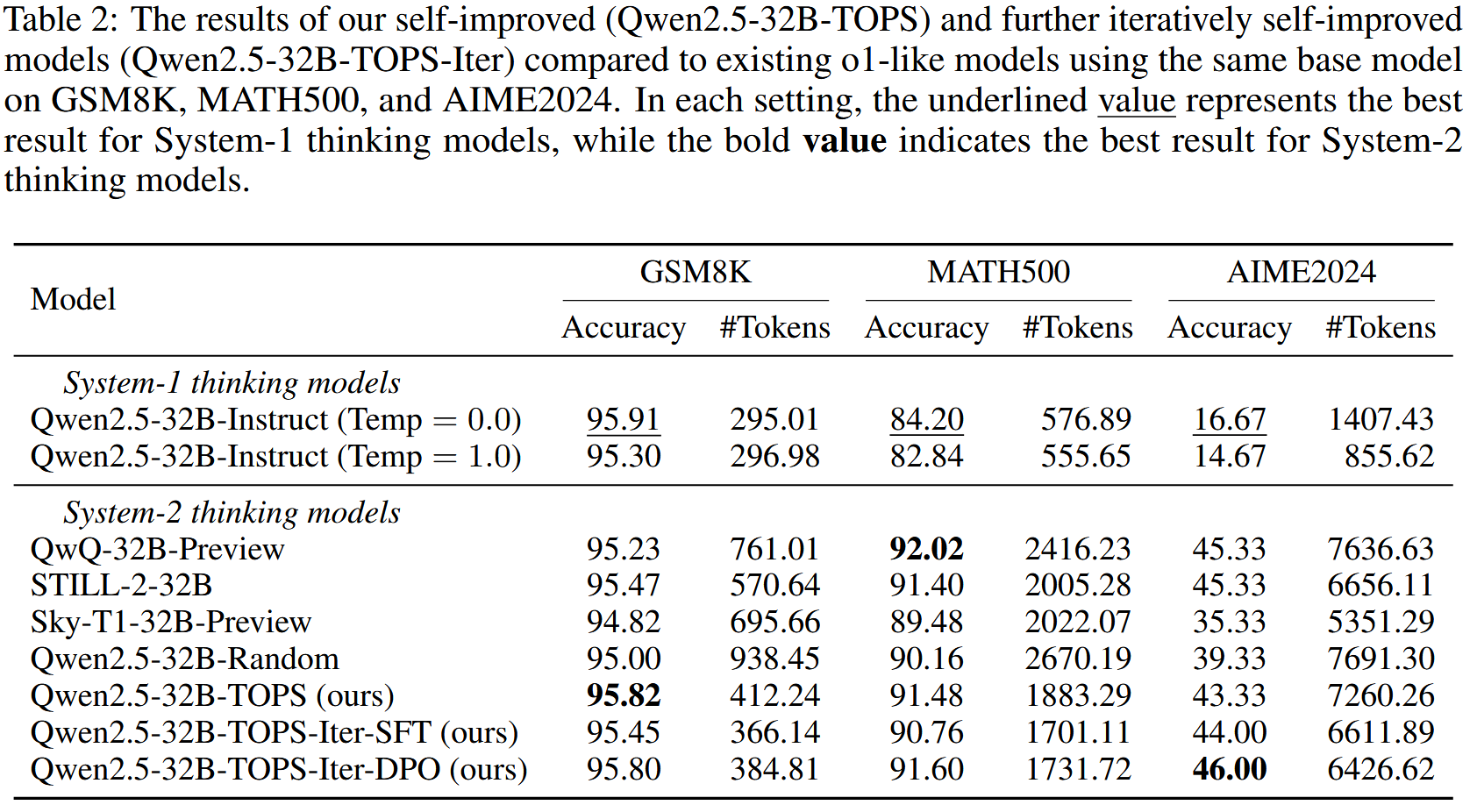
简单问题上 Token 少了
Baseline
- QwQ-32B-Preview
- STILL-2-32B:一个基于 QwQ-32B-Preview 和 DeepSeek-R1-Lite 生成的 3.9K 个具有挑战性的数学例子训练的 System-2 思维模型
- Sky-T1-32B-Preview:训练使用的推理模型基于 QwQ-32B-Preview 生成的 17K 个样本,其中包括 10K 个数学示例。
- Qwen2.5-32B-Random:在 tag 模型基于推理努力生成解之后,我们在每个问题上随机选择一个正确的解而不是最短的解来构建思维次优数据集,并在此数据集上训练基础模型。
为了进一步提升模型在具有挑战性问题上的推理性能,我们在 Qwen2.5-32B-TOPS 上进行迭代自改进。具体而言,我们选择了额外的 4500 个 MATH 问题[13](这些问题是之前使用的问题中未出现过的)以及 AIME1983-2023 的问题。对于每个问题,我们从 Qwen2.5-32B-TOPS 采样 8 个响应。然后,在这 8 个响应中选择最短的正确响应作为选定响应。一种迭代自改进的方法是对由所有选定响应(最短正确响应)组成的数据集进一步监督微调 Qwen2.5-32B-TOPS,从而得到 Qwen2.5-32B-TOPSIter-SFT。此外,我们还可以执行偏好优化。具体来说,如果有最终答案错误的响应,我们选择最长的错误响应作为拒绝响应以提高推理能力。另外,如果存在比最短正确响应更短的错误响应,我们将这些错误响应中最短的一个作为拒绝响应,并包含这些偏好对,以避免模型思考不足。在获得偏好数据集后,我们在 Qwen2.5-32B-TOPS 上进行直接偏好优化(DPO)[28],得到 Qwen2.5-32BTOPS-Iter-DPO。