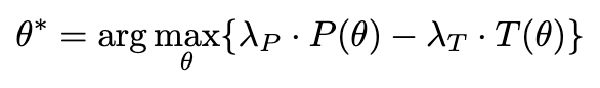Hmm 等 Token 影响模型推理能力#
Demystifying Reasoning Dynamics with Mutual Information: Thinking Tokens are Information Peaks in LLM Reasoning
感觉 Motivation 阐述的不是很明确,但是想法的不错
但是工程方面似乎有些问题,详情请看下面的高亮块
摘要#
大规模推理模型(LRMs)在复杂问题求解方面展现出了令人印象深刻的能力,但其内部的推理机制仍缺乏深入理解。本文从信息论的角度出发,研究了 LRMs 的推理轨迹。通过追踪中间表示与正确答案之间的互信息(MI)在 LRM 推理过程中如何演变,我们观察到一种有趣的 MI 峰值现象:在某些特定生成步骤中,MI 会在 LRM 的推理过程中突然且显著地增加。我们对该现象进行了理论分析,并证明随着 MI 的增加,模型预测错误的概率会下降。此外,这些 MI 峰值通常对应于表达思考或转折的词元(token),例如“Hmm”、“Wait”和“Therefore”,我们将这类词元称为思考词元(thinking tokens)。接着我们表明,这些思考词元对 LRM 的推理性能至关重要,而其他词元则影响甚微。基于这些分析,我们提出了两种简单但有效的改进方法,通过精心利用这些思考词元来提升 LRM 的推理表现。总体而言,本研究为理解 LRMs 的推理机制提供了新的视角,并为提升其推理能力提供了可行的实践路径。代码地址为 https://github.com/ChnQ/MI-Peaks。
Motivation#
- 尽管最近的逻辑推理模型(LRMs)如 DeepSeek 的 R1 系列模型[18]和 Qwen 的 QwQ[42]展现出了令人印象深刻的推理能力,但驱动这些能力的基本机制仍缺乏清晰的理解。
一些发现#
截止目前,LRM 内部的推理的动态仍然是不可知的。且一些研究表明 LRM 的某些关键 token 会严重影响模型生成内容的安全性,所以作者希望弄清楚:
- 在 LRMs 的推理过程中,是否存在显著影响最终结果的关键推理步骤或中间状态?
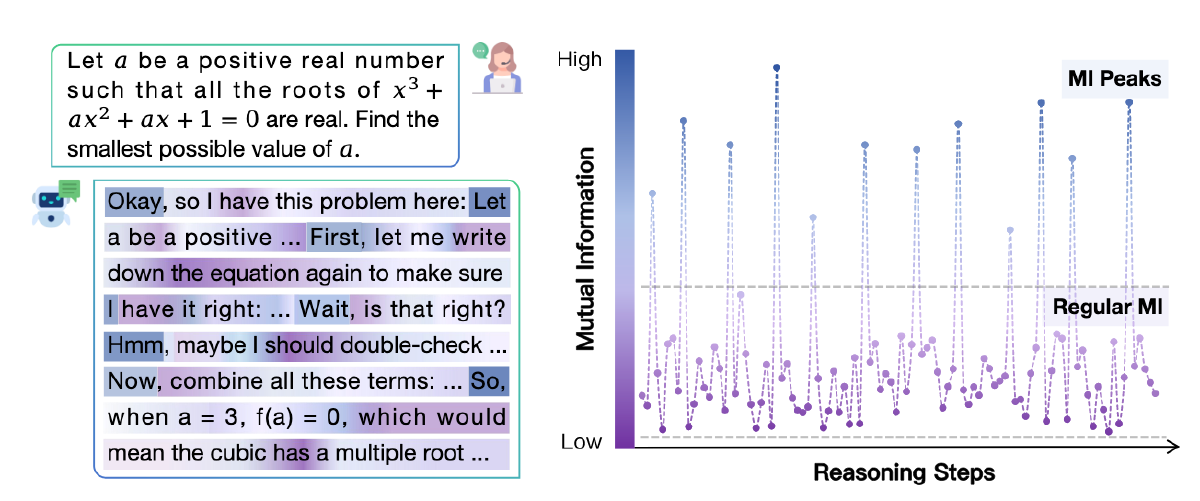
实验发现模型的中间步骤与 gold answer 之间的互信峰值的分布是稀疏且不均匀的
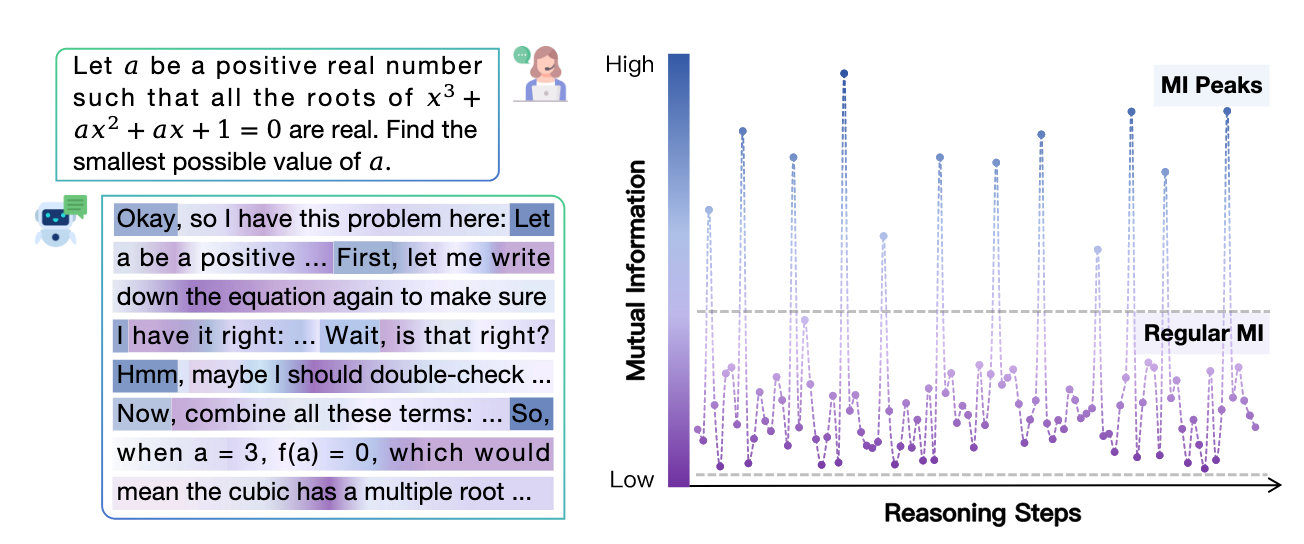
这表明在某些关键的推理步骤中,LRMs 的表示变得对正确答案影响较大。于是又提出另一个问题:
- 这些 MI(互信度)峰值是否可能与模型的推理性能相关?
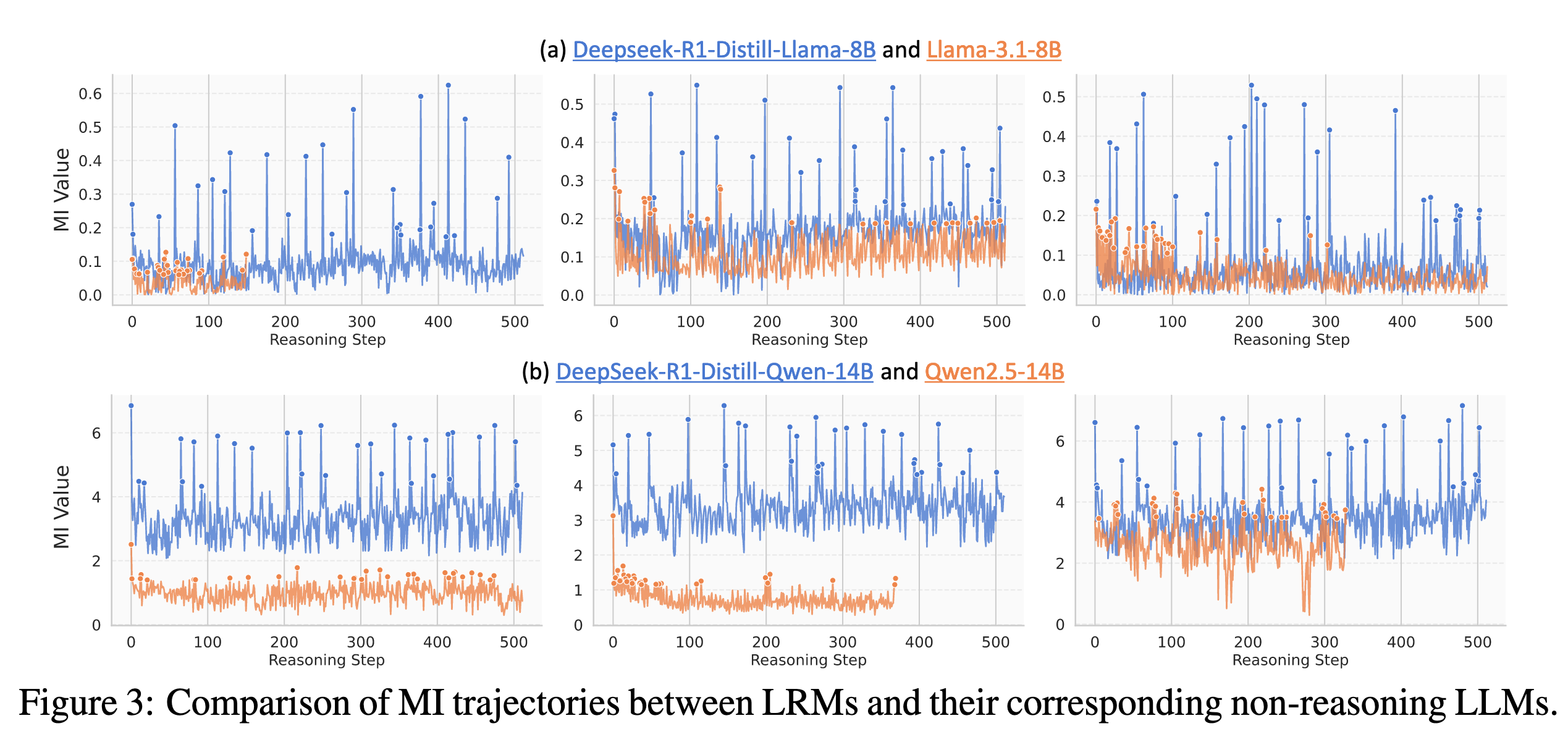
作者继续实验,发现当 LRM 的输出与 ground truth 之间的累积互信度增加时,LRM 的推理出错的概率会降低。但是 LRM 所对应的基座模型就没表现出这么明显的峰值现象。所以作者认为峰值现象的出现可能源于密集的推理训练,并且可能和 LRM 卓越的推理能力相关
于是提出第三个问题:
- 在推理过程中,MI 峰值处的表示承担了哪些语义角色?
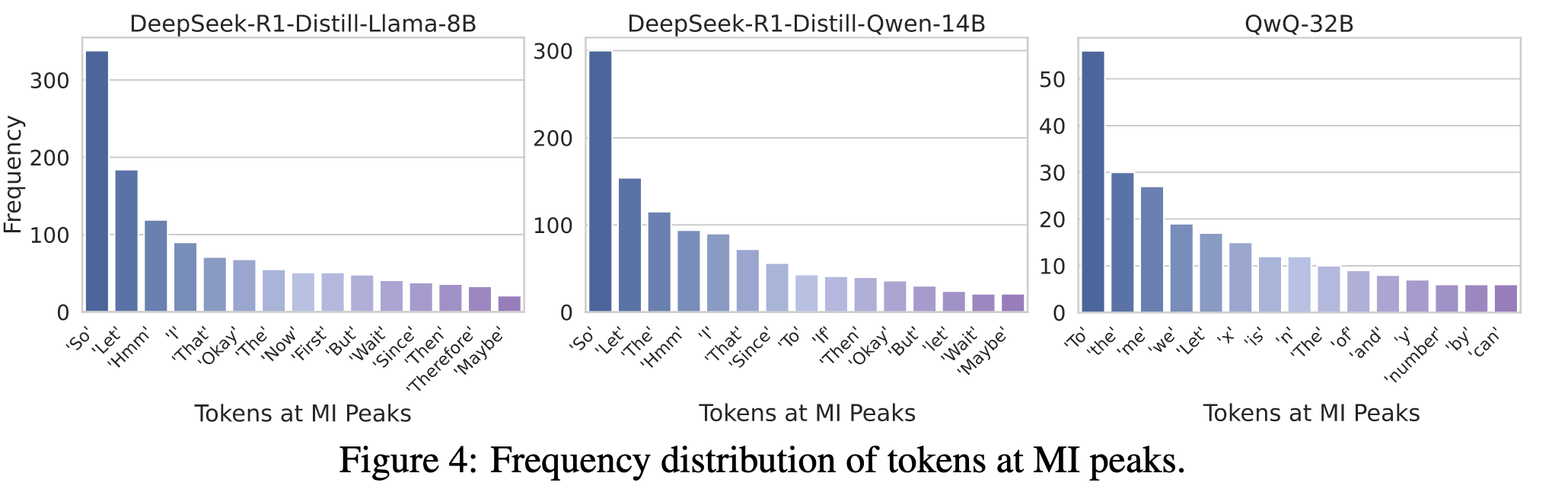
发现这些具有互信息(MI)峰值的表示主要对应于诸如“Wait”、“Hmm”、“Therefore”、“So”之类的词符(token),这些词通常表达沉思、自我纠正或转折过渡的含义。

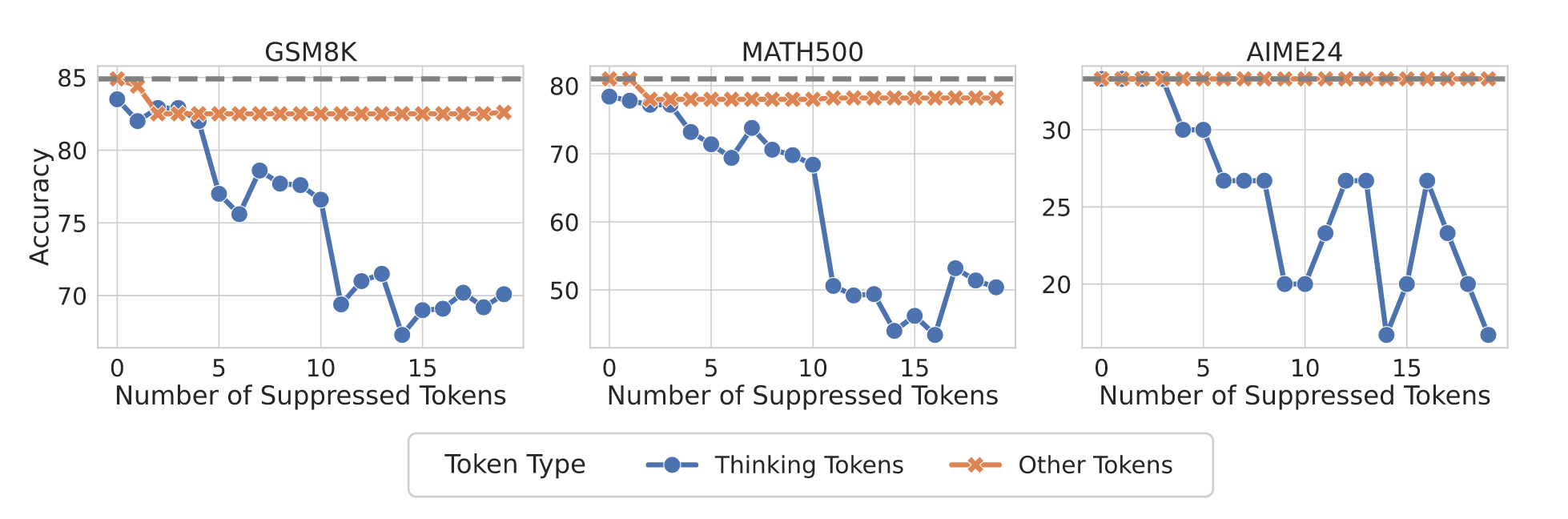
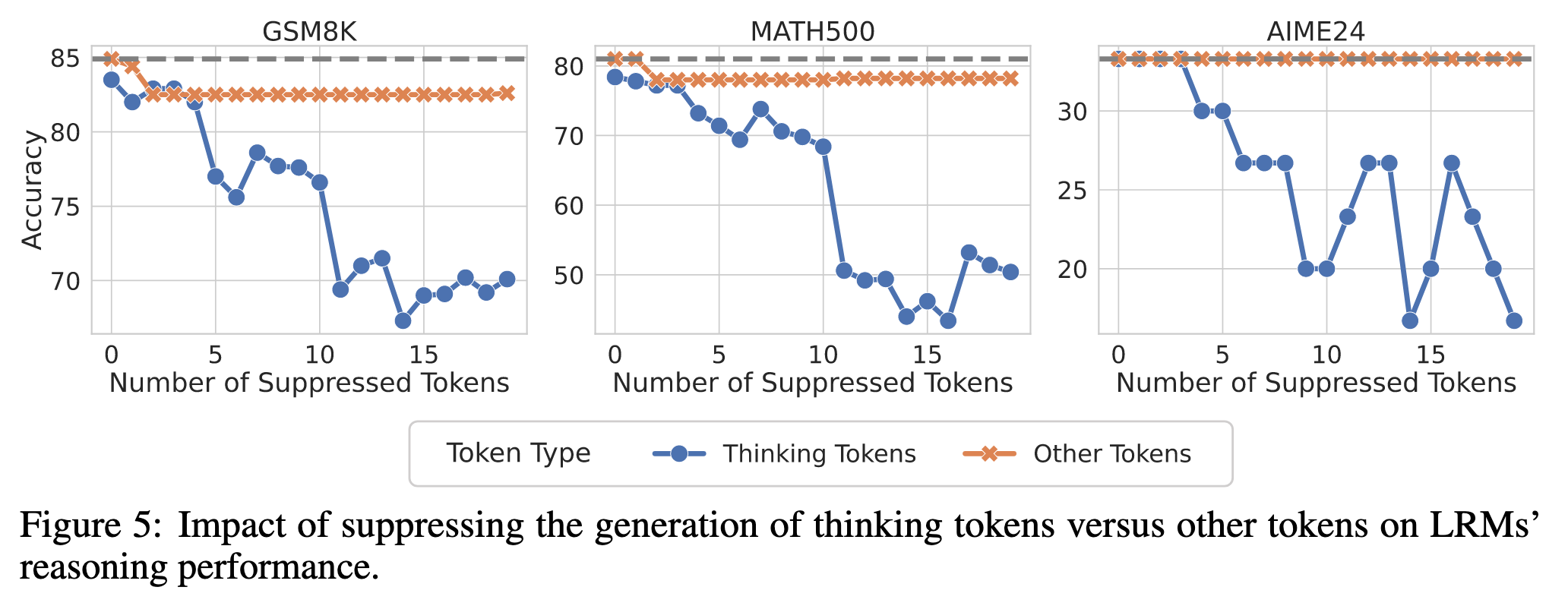
作者将上述具有 MI 峰值的 token 命名为 thinking token,并假设这些思考 token 可能在模型的推理能力中发挥了关键作用,为了验证以上猜想,作者在某次实验中抑制了 thinking token 的生成,并且发现这样做显著损害的模型性能。且如果抑制的是其他 token,则没有明显的区别
Contributions#
提出了两种 Training free 的提高 LRM ACC 的方法:
- 表示循环(Representation Recycling, RR)方法。RR 鼓励模型更好地利用这些具有信息量的表示
- 基于思考 token 的测试时扩展方法(Thinking Token based Test-time Scaling, TTTS)。具体而言,当存在额外的 token 预算时,我们强制模型从思考 token 开始继续进行推理。
模型 MI 峰值现象#
方法#
MI 峰值的出现#
将一个数据集的 X 输入的 Model 中,获得 T 个输出 Token(Y’),并且收集每个 token 对应的 hidden state,设 A 为提取 hidden state 的函数,这个过程记为:
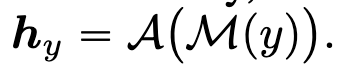
各个 Token 和 gold answer 间的 MI#
在提取表示之后,我们随后度量每个生成 token 的隐藏状态 ht 与标准答案的隐藏状态 hy 之间的互信息(MI),从而获得一个 MI 序列:[(ht; hy), I(ht; hy), …, I(ht; hy)]。
是怎么获得到 hy 的呢? 看代码得知,LRM 没使用任何 template(hy 和 ht 都没有),直接将 ground truth 输入到 LRM 中,并提取出对应的几个 token 的 hidden state hy 没使用任何 template 也可以理解,毕竟不希望 template 中的内容干扰 hy 但是为什么 ht 也不应用 template 呢?
对于 ht 的问题我已经在 github 上提问了,尚未得到答复
计算 MI#
采用希尔伯特-施密特独立性指标,用于衡量两个变量之间的独立性
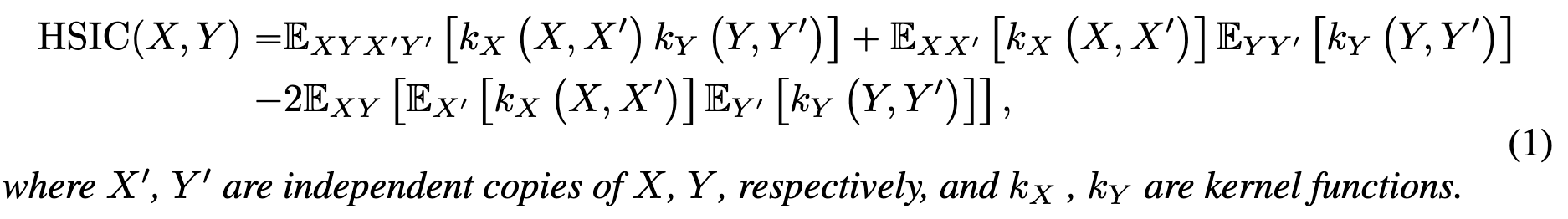
峰值定义#
对于一个 MI 序列,定义 Q1 和 Q3 是其中两端的两个四分位点,定义 IQR(m)=Q3-Q1 为四分位距,定义峰值为:
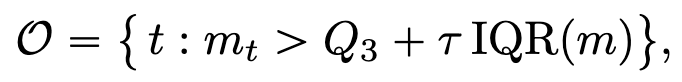
其中 τ 为超参数,实验中设置为 1.5
实验#
在 MATH 数据集上实验,MI 是稀疏的、不均匀的
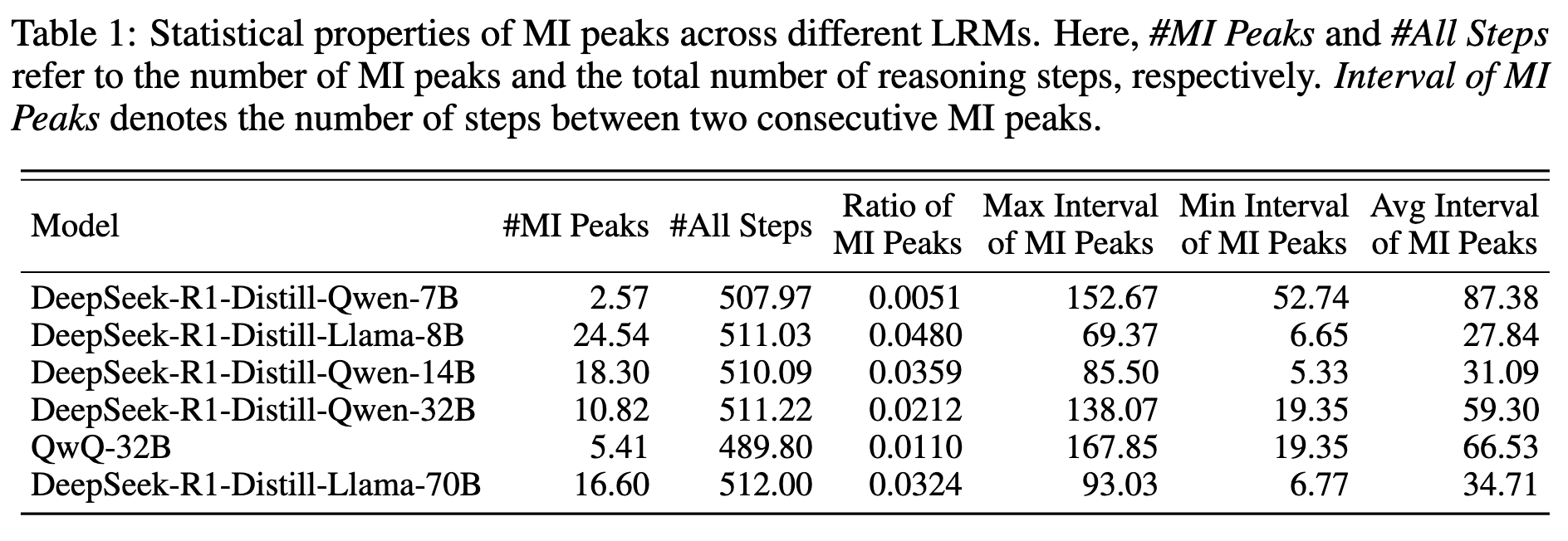
MI 峰值导致模型出错的概率边界越窄#
作者想知道,MI 峰值和 Acc 的关系
- 定理 1.,设模型共生成 T 个 token,Pe 是模型出错的概率则有
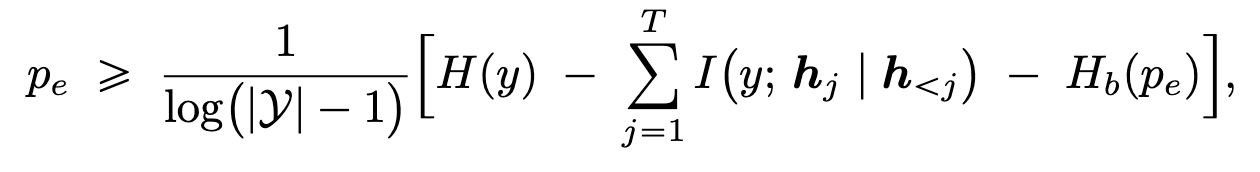
其中 Hb 为二元熵:
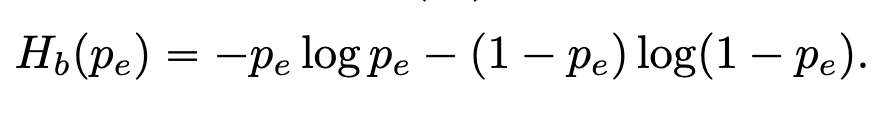
- 定理 2,
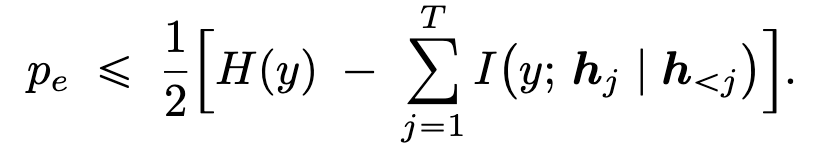
作者声称定理 1 建立了 LLM 预测误差 pe 的下界。直观上,它表明若要 LLM 实现较低的误差率,其在生成过程中的一系列内部表示应能够捕捉关于正确答案的更多信息。换句话说,在生成轨迹中保持较高的互信息(MI)可能有助于降低模型可达到的最小误差。定理 2 给出了预测误差 pe 的一个上界,这补充了定理 1 中的下界。它表明,表示序列与正确答案之间的累积互信息(MI)越高,大语言模型(LLM)误差概率的上界就越紧。
非推理模型的 MI 峰值 Weaker 且 Less#
MI 峰值所对应的 token 的语义特征#
直接将上述推理的结果 decode 出来,发现在 MI 峰值处出现的 token 主要是表达自我反思或 LRM 推理过程中转折的连接词。作者定义这些 token 为 thinking token
MI 峰值对于 LRM 的推理的重要性#
抑制 thinking token 的出现会大大影响 Acc,而抑制普通 token 的出现不会
抑制 thinking token 的方法是在生成过程中将其概率设置为 0,导致无法采样到想要抑制的 token
抑制普通 token 的方法是随机采样一些 token,并将其概率设置为 0
作者对于抑制 thinking token 的方法并非严格递减的解释如下,有时抑制 Wait,模型会生成 But wait 短语来规避这种抑制
应用上述发现提升 LRM 推理能力#
推理过程中高互信息表示的再利用(RR)#
方法#
对于 Thinking Token,将其对应的 hidden state 在某一层处理两次再传递给下一层
例如普通 Token 在第 l 层的处理为:\(h_l=TF_l{h_{l-1}}\),但对于 Thinking Token 在第 l 层的处理就是 \({h'}_l=TF_l{h_{l-1}},h_l=TF_l{{h'}_l}\),但是对于其他层都是常规处理
实验#
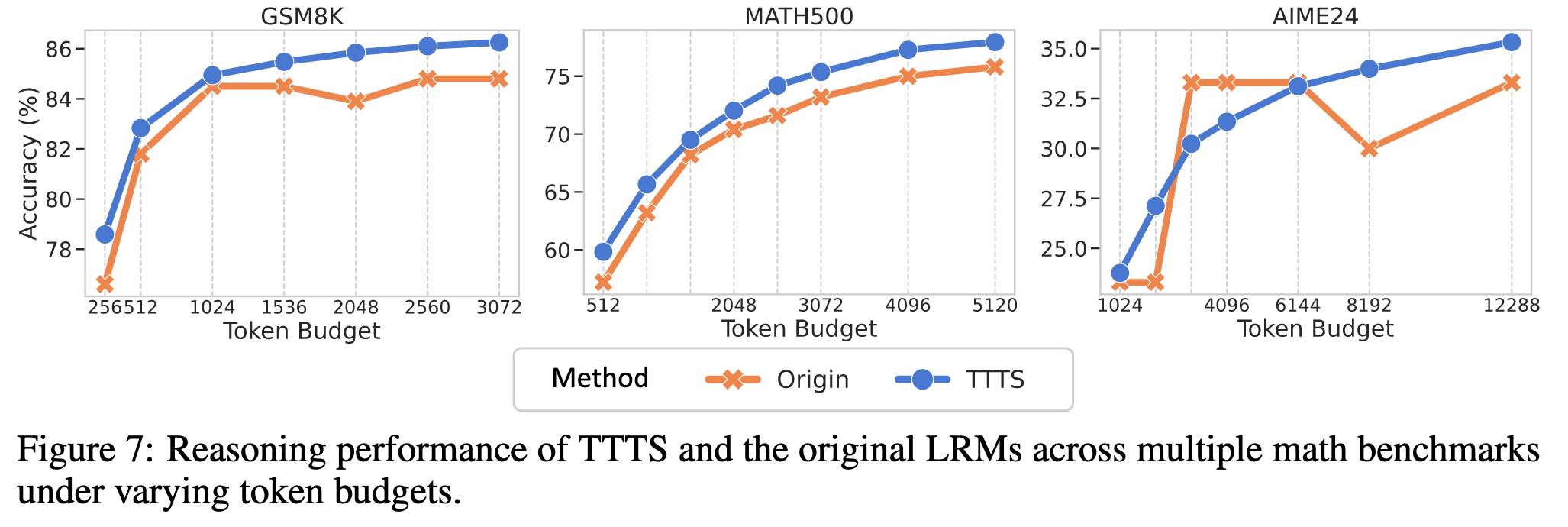
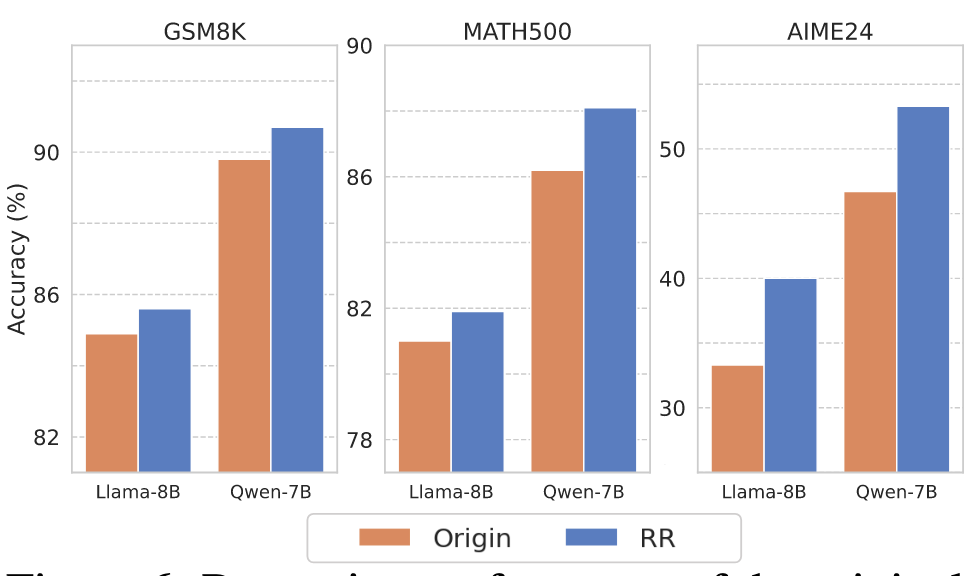
为了评估 RR 的有效性,我们在三个数学推理基准测试中使用 DeepSeek-R1-Distill-Llama-8B 和 DeepSeek-R1-Distill-Qwen7B 进行实验。由于在推理过程中无法获取真实答案,我们首先使用 MATH 数据集的训练集记录思维 token(如第 3.1 节所述),然后当模型生成这些思维 token 之一时触发 RR。基于以往研究建议,LLMs 的中间层或高层倾向于编码更具语义丰富的内容,因此我们经验性地将 l 设置为这些层次。
没介绍实验中具体取的哪一层
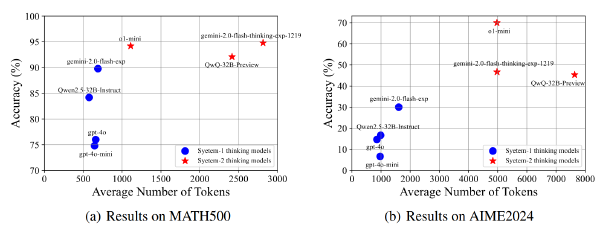
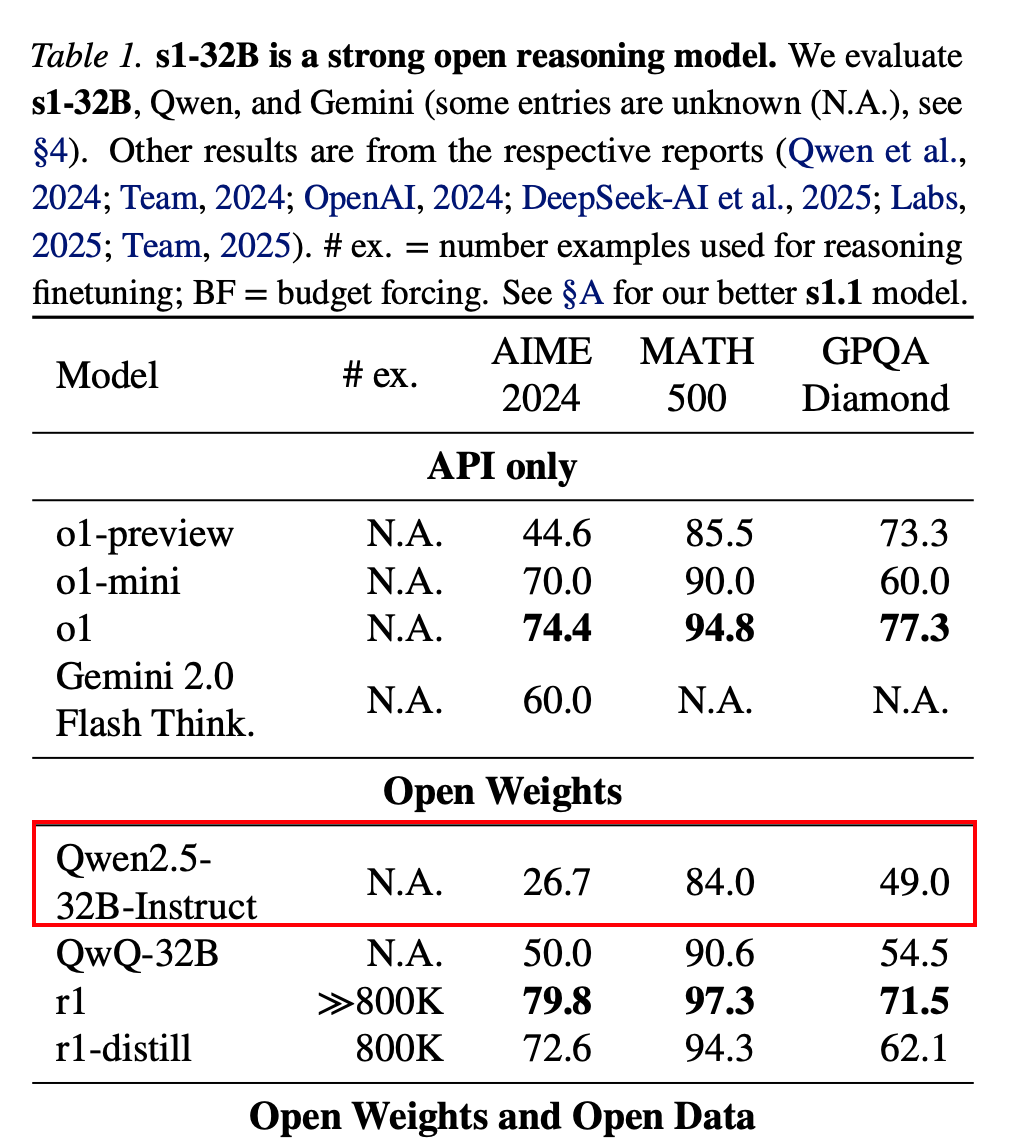
以下是另外一篇文章汇报的 Qwen25-32b-instruct 的结果,感觉可能和 sampling 策略有关,我采用的是 temperate,这些论文似乎更倾向于 greedy
Test-Time Scaling with Thinking Tokens#
方法#
基于上面识别出的思维 token 集合,我们过滤掉语义内容较少的 token(例如标点符号和单个字符),并保留诸如“So,”、“Hmm,”之类的 token,这些 token 通常表示思考、过渡或进一步推理的开始。然后在推理过程中,我们将其中一个思维 token 附加到模型初始输出的末尾,并允许其继续生成额外的推理步骤。
实验#